
 B .
B .  C .
C .  D .
D . 
求作:直线 , 使其过点
, 并与
相切.
作法:①连接;
②分别以点 , 点
为圆心,
长为半径作弧,两弧交于
外一点
;
③作直线 .
直线就是所求作直线
.
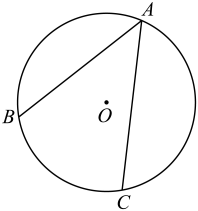
证明:连接 ,
,
∵ ,
∴四边形是菱形,
∵点 ,
,
在
上,且
,
∴ ▲ °( )(填推理的依据).
∴四边形是正方形,
∴ , 即
,
∵为
半径,
∴直线为
的切线( )(填推理的依据).
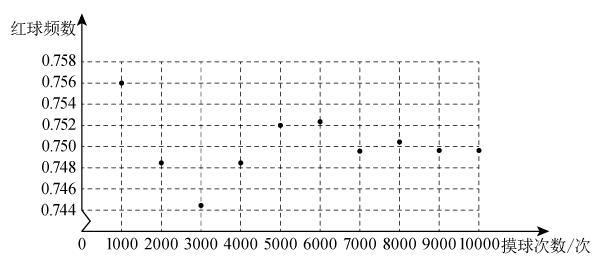
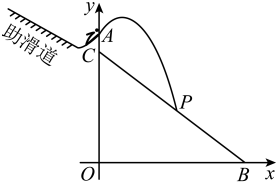
①若点与点
关于
双对合,求
的取值范围;
②当点运动时,若
上存在一点与
上任意一点关于
双对合,直接写出点
的横坐标
的取值范围.