题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

人教版七年级上线段动点专题训练

更新时间：2023-02-14 浏览次数：234 类型：复习试卷

一、综合题

1. (2022七上·汽开区期中) 已知在数轴上点M、N表示的数分别为a，b，点M、N两点之间的距离表示为 $\text{[math]}$ 或 $\text{[math]}$ ，记为 $\text{[math]}$ ．如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．点P是数轴上任意一点，
1. （1）数轴上点B表示的数是；
2. （2）如果点P到点A、点B的距离相等，那么点P表示的数是；
3. （3）若点P到点A、点B的距离之和等于14，则点P表示的数为；
4. （4）若点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动．动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，运动时间为t．求：
  ①当 $\text{[math]}$ 秒时P，Q两点间的距离为 ▲ ；
  
  ②当点P运动多少秒时，点P与点Q相遇？
  
  ③当点P与点Q间的距离为8个单位长度时t的值为 ▲ ．
答案解析收藏纠错 + 选题
2. (2022七上·慈溪月考) 如图1，已知数轴上有三个点A，B，C，它们对应的数分别为 $\text{[math]}$ ，且 $\text{[math]}$ ，点C对应的数是10.
1. （1）若BC=15，求 $\text{[math]}$
  图1
2. （2）如图2，在（1）的条件下，O为原点，动点P，Q分别从点A，C同时出发，点P向左运动，运动速度为每秒2个单位长度，点Q向右运动，运动速度为每秒1个单位长度，N为OP的中点，M为BQ的中点.
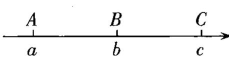
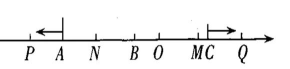  图2
  
  用含t的代数式表示PQ，MN.
  
  在点P，Q的运动过程中，PQ与MN存在一个确定的等量关系，请指出它们之间的关系，并说明理由.
答案解析收藏纠错 + 选题
3. (2021七上·南山期末) 如图，P是线段AB上不同于点A，B的一点，AB＝18cm，C，D两动点分别从点P，B同时出发，在线段AB上向左运动（无论谁先到达A点，均停止运动），点C的运动速度为1cm/s，点D的运动速度为2cm/s．
1. （1）若AP＝PB，
  ①当动点C，D运动了2s时，AC＋PD＝cm；
  
  ②当C，D两点间的距离为5cm时，则运动的时间为s；
2. （2）当点C，D在运动时，总有PD＝2AC，·
  ①求AP的长度；
  ②若在直线AB上存在一点Q，使AQ﹣BQ＝PQ，求PQ的长度．
答案解析收藏纠错 + 选题
4. (2021七上·平阴期末) [背景知识]
1. （1）数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：若数轴上点A、点B表示的数分别为a、b，则A，B两点之间的距离AB＝|a－b|，线段AB的中点表示的数为；
2. （2） [问题情境]
  如图，数轴上点A表示的数为－2，点B表示的数为8，点P从点A出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动，设运动时间为t秒（t＞0）．
  线段AB的中点表示的数为；
3. （3） [综合运用]
  求当t为何值时PQ＝ $\text{[math]}$ AB；
4. （4）若点M为PA的中点，点N为PB的中点，点P在运动过程中，线段MN的长度是否发生变化?若变化，请说明理由；若不变，请求出线段MN的长．
答案解析收藏纠错 + 选题
5. (2022七上·金乡县期末) 【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：若数轴上点A、点B表示的数分别为a、b，则A，B两点之间的距离AB= $\text{[math]}$ ，线段AB的中点表示的数为 $\text{[math]}$ ．如图，数轴上点A表示的数为 $\text{[math]}$ ，点B表示的数为8．
1. （1）【综合运用】
  填空：A，B两点间的距离AB=，线段AB的中点表示的数为；
2. （2）若M为该数轴上的一点，且满足MA+MB=12，求点M所表示的数；
3. （3）若点P从点A出发，以每秒1个单位长度的速度沿数轴向终点B匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动，Q到达A点后，再立即以同样的速度返回B点，当点P到达终点后，P、Q两点都停止运动，设运动时间为t秒（ $\text{[math]}$ ）．当t为何值时，P，Q两点间距离为4．
答案解析收藏纠错 + 选题
6. (2022七上·抚州期末) 如图1，A，B两点在数轴上对应的数分别为-12和 4．
1. （1） A，B两点之间的距离为；
2. （2）若在数轴上存在一点P，使得 $\text{[math]}$ ，求点P表示的数．
3. （3）如图2，现有动点P，Q，若点P从点A出发，以每秒5个单位长度的速度沿数轴向右运动，同时点Q从点B出发，以每秒1个单位长度的速度沿数轴向左运动，当点Q到达原点O后立即以每秒3个单位长度的速度沿数轴向右运动，设运动时间为t秒．求：当 $\text{[math]}$ 时t的值．
答案解析收藏纠错 + 选题
7. (2022七上·阿鲁科尔沁旗期末) 如图，在数轴上，O为原点，点A表示的数为－10，点B表示的数为4．
1. （1） A，B两点间的距离是．
2. （2）若将数轴折叠，使得点A与点B重合，此时原点O与表示数的点重合．
3. （3）若点A，B分别以每秒1个单位长度和每秒3个单位长度的速度同时向左运动，则几秒时点B追上点A？
4. （4）若点A，B以（3）中的速度相向而行，则几秒时A，B两点相距2个单位长度？
答案解析收藏纠错 + 选题
8. (2021七上·镇江期末) 如图，线段 $\text{[math]}$ 厘米，点D和点C在线段AB上，且 $\text{[math]}$ ， $\text{[math]}$ .点P从点A出发以4厘米/秒的速度沿射线AD向点C运动，点P到达点C所在位置后立即按照原路原速返回，到达点D所在位置后停止运动，点Q从点B出发以1厘米/秒的速度沿着射线BC的方向运动，点Q到达点D所在的位置后停止运动.点P和点Q同时出发，点Q运动的时间为t秒.
1. （1）求线段AD的长度；
2. （2）当点C恰好为PQ的中点时，求t的值；
3. （3）当 $\text{[math]}$ 厘米时，求t的值.
答案解析收藏纠错 + 选题
9. (2021七上·蓬江期末) 如图，已知A，B两点在数轴上，点A表示的数为−15，OB=2OA，点M以每秒3个单位长度的速度从点A向右运动．点N以每秒2个单位长度的速度从点O向右运动（点M、点N同时出发）
1. （1）数轴上点B对应的数是；
2. （2）经过几秒，点M、点N到原点O的距离相等？
3. （3）当点M运动到什么位置时，恰好使AM=3BN？
答案解析收藏纠错 + 选题
10. (2021七上·法库期末) 如图，已知数轴上点A，O，B对应的数分别为 $\text{[math]}$ ， 0，6，点P是数轴上的一个动点．
1. （1）设点P对应的数为x．
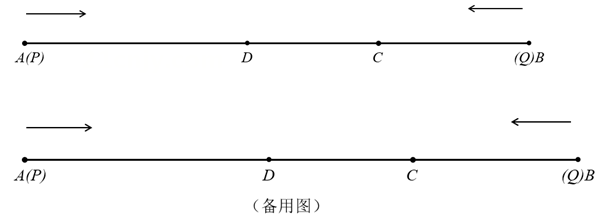
  ①若点P到点A和点B的距离相等，则x的值是；
  
  ②若点P在点A的左侧，则 $\text{[math]}$ ， $\text{[math]}$ （用含x的式子表示）；
2. （2）若点P以每秒1个单位长度的速度从点O向右运动，同时点A以每秒3个单位长度的速度向左运动，点B以每秒6个单位长度的速度向右运动，在运动过程中，点M和点N分别是 $\text{[math]}$ 和 $\text{[math]}$ 的中点，设运动时间为t．
  ①移动后，点P在数轴上所表示的数为 ▲ ，点A在数轴上所表示的数为 ▲ ，点B在数轴上所表示的数为 ▲ ，（用含t的式子表示）；
  
  ②求 $\text{[math]}$ 的长（用含的式子表示）；
  
  ③当 $\text{[math]}$ ▲ 时， $\text{[math]}$ ．
答案解析收藏纠错 + 选题
11. (2021七上·伊通期末) 如图，在数轴上有A、B、C三点，A、B两点所对应的数分别是a，b，且满足a+5是最大的负整数，b﹣3是绝对值最小的有理数，点C在点A的右侧，到点A的距离是2个单位长度．请你解答下列问题：
1. （1）点A表示的数是，点B表示的数是，点C表示的数是；
2. （2）点P、Q为数轴上两个动点，点P从A点出发速度为每秒1个单位长度，点Q从B点出发速度为每秒2个单位长度，若P、Q两点同时出发，相向而行，运动时间为t秒．求当t为何值时，点P与点Q之间的距离是3个单位长度？
3. （3）在（2）的条件下，当点P与点Q之间的距离是3个单位长度时，请你直接写出点C与点Q的距离．
答案解析收藏纠错 + 选题
12. (2021七上·绿园期末) 如图，数轴上点A表示－10，点O表示0，点B表示10，点C表示18.动点P从点A出发，以2单位/秒的速度沿着数轴的正方向运动；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动．当点Р到达点C时，两点都停止运动．设点P运动的时间为t（秒）．
1. （1）点A和点C在数轴上相距个单位．
2. （2）当 $\text{[math]}$ 时，求点P与点Q的距离．
3. （3）求P、Q两点相遇时t的值．
4. （4）当线段PO与线段QB的长度相等时，直接写出t的值．
答案解析收藏纠错 + 选题
13. (2021七上·铁西期中) 如图，点A在数轴上所对应的数为2，
1. （1）点B在点A左侧且距点A为3个单位长度，则点B所对应的数为，请在数轴上标出点B的位置；
2. （2）在（1）的条件下，点A以每秒1个单位长度沿数轴向右运动，点B以每秒2个单位长度沿数轴向左运动，当点A运动到5所在的点处时停止运动，同时点B也停止运动，求此时A，B两点间距离；
3. （3）在（2）的条件下，若点A不动，点B沿数轴向右运动，经过t秒A，B两点相距3个单位长度，求t值；
4. （4）在（1）的条件下，点A以每秒1个单位长度，点B以每秒2个单位长度同时沿数轴向左运动，当点B运动到所对应的数为m时停止运动，请直接写出此时点A所对应的数为；若点A继续运动，请直接写出当AB＝2时，点A继续运动的距离为．（用含m的式子表示）
答案解析收藏纠错 + 选题
14. (2021七上·黄冈期中) 如图，已知数轴上有 $\text{[math]}$ 三点，分别表示有理数 $\text{[math]}$ ，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒1个单位的速度向终点 $\text{[math]}$ 移动，当点 $\text{[math]}$ 运动到 $\text{[math]}$ 点时，点 $\text{[math]}$ 从 $\text{[math]}$ 点出发，以每秒3个单位的速度向 $\text{[math]}$ 点运动.
1. （1） $\text{[math]}$ 点出发3秒后所到的点表示的数为，此时 $\text{[math]}$ 两点的距离为.
2. （2）问当点 $\text{[math]}$ 从点 $\text{[math]}$ 点出发几秒钟时，能追上点 $\text{[math]}$ ？
3. （3）问当点 $\text{[math]}$ 从点 $\text{[math]}$ 点出发几秒钟时，点 $\text{[math]}$ 和点 $\text{[math]}$ 相距2个单位长度？直接写出此时点 $\text{[math]}$ 在数轴上表示的有理数.
答案解析收藏纠错 + 选题
15. (2021七上·禹城期中) 如图，在数轴上点A，B，C表述的数分别为 $\text{[math]}$ 、1、6，点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，点A与点C之间的距离表示为AC．
1. （1）请直接写出AB、BC、AC的长度；
2. （2）若点D从A点出发，以每秒1个单位长度的速度向左运动，点E从B点出发以每秒2个单位长度的速度向右运动，点F从C点出发以每秒5个单位速度向右运动．设点D、E、F同时出发，运动时间为t秒．
  ①t秒后，D表示的数为 ▲ ， E表示的数为 ▲ ， F表示的数为 ▲ ．
  
  ②试探索： $\text{[math]}$ 的值是否随着时间t的变化而变化？请说明理由．
3. （3）若点M以每秒4个单位的速度从A点出发，点N以每秒3个单位的速度运动从C点出发，设点M、N同时出发，运动时间为t秒．试探究：经过多少秒后，点M、N两点间的距离为14个单位．
答案解析收藏纠错 + 选题

试卷信息