江苏省宿迁青华中学2022-2023学年九年级下学期开学考试...

更新时间：2024-07-31 浏览次数：88 类型：开学考试

一、单选题

1. (2024九上·任丘期中) 如果3x＝4y（y≠0），那么下列比例式中成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九下·宿迁开学考) 二次函数y＝x²-2x+3的图象的顶点坐标是（）

A . （1，6） B . （1，2） C . （-1，6） D . （-1，2）

答案解析收藏纠错 + 选题
3. (2023九下·宿迁开学考) 已知：在Rt△ABC中，∠C=90°，sinA= $\text{[math]}$ ，则cosB的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九下·宿迁开学考) 若关于x的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，则实数k的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九下·宿迁开学考) 如图，在半径为5的⊙O中，弦AB＝6，OP⊥AB，垂足为点P，则OP的长为（）

A . 2.5 B . 3 C . 3.5 D . 4

答案解析收藏纠错 + 选题
6. (2023九下·宿迁开学考) 设A（1，y₁），B（﹣2，y₂）是抛物线y＝﹣（x+1）²+a上的两点，则y₁、y₂的大小关系为（）

A . y₁＜y₂ B . y₁＞y₂ C . y₁≤y₂ D . y₁≥y₂

答案解析收藏纠错 + 选题
7. (2023九下·宿迁开学考) 如图，点A，B，C，D，E在⊙O上， $\text{[math]}$ 的度数为60°，则∠B+∠D的度数是（）

A . 180° B . 120° C . 100° D . 150°

答案解析收藏纠错 + 选题
8. (2023九上·余姚期中) 如图，点A ， B的坐标分别为 $\text{[math]}$ ，点C为坐标平面内一点， $\text{[math]}$ ，点M为线段 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2023九下·宿迁开学考) 如果 $\text{[math]}$ ，那么锐角 $\text{[math]}$ 的度数为°.

答案解析收藏纠错 + 选题
10. (2024九上·钦州月考) 经过两次连续降价，某药品销售单价由原来的50元降到32元，设该药品平均每次降价的百分率为x，根据题意可列方程是．

答案解析收藏纠错 + 选题
11. (2023九下·宿迁开学考) 如图，直线l₁∥l₂∥l₃ ，直线AC分别交l₁、l₂、l₃于点A、B、C，直线DF分别交l₁、l₂、l₃于点D、E、F，若AB＝3，BC＝5，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
12. (2023九下·宿迁开学考) 如图，抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于 $\text{[math]}$ 两点，则不等式 $\text{[math]}$ 的解集是.

答案解析收藏纠错 + 选题
13. (2023九下·宿迁开学考) 已知点M为线段AB的黄金分割点，且 $\text{[math]}$ ，若 $\text{[math]}$ ，则AM=cm．

答案解析收藏纠错 + 选题
14. (2023九下·宿迁开学考) 如图，边长为1的小正方形网格中，点 $\text{[math]}$ 均在格点上，半径为2的 $\text{[math]}$ 与 $\text{[math]}$ 交于点F，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024九上·长春汽车经济技术开发期末) 如图，AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上，斜边过点B，一条直角边交该半圆于点Q. 若AB=4，则弧BQ的长为.

答案解析收藏纠错 + 选题
16. (2023九下·宿迁开学考) 如图，D、E分别是 $\text{[math]}$ 的边 $\text{[math]}$ 上的点， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
17. (2023九下·宿迁开学考) 如下图，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ 下列判断：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ .其中判断一定正确的序号是.

答案解析收藏纠错 + 选题
18. (2023九下·宿迁开学考) 如图，矩形OABC中，O为坐标原点，点A、点C分别落在x轴、y轴上，点B坐标为（4，6），点D为AB边中点，点E为射线BC上的一个动点，将△BDE沿DE折叠，点B的对应点为点B＇，连接OB＇，当OB＇长度最小时点B＇的坐标为.

答案解析收藏纠错 + 选题

三、解答题

19. (2024九下·凉州模拟) 解方程或计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2023九下·宿迁开学考) 已知如图，Rt△ABC中，∠C＝90°，CD是斜边上的高，求证：CD²＝AD•BD.

答案解析收藏纠错 + 选题
21. (2023九下·宿迁开学考) 在全运会射击比赛的选拔赛中，运动员甲10次射击成绩的统计表和扇形统计图如下：
命中环数
10
9
8
7
命中次数
▲
3
2
▲
1. （1）根据统计表(图)中提供的信息，补全统计表及扇形统计图；
2. （2）已知乙运动员10次射击的平均成绩为9环，方差为1.2，如果只能选一人参加比赛，你认为应该派谁去？并说明理由.
答案解析收藏纠错 + 选题
22. (2023九下·宿迁开学考) 九年级某班要召开一次“走近抗疫英雄，讲好中国故事”主题班会活动，李老师制作了编号为A、B、C、D的4张卡片（如图，除编号和内容外，其余完全相同），并将它们背面朝上洗匀后放在桌面上．
1. （1）小明随机抽取1张卡片，抽到卡片编号为B的概率为；
2. （2）小明从4张卡片中随机抽取1张（不放回），小丽再从余下的3张卡片中随机抽取1张，然后根据抽取的卡片讲述相关英雄的故事，求小明、小丽两人中恰好有一人讲述钟南山抗疫故事的概率（请用“画树状图”或“列表”等方法写出分析过程）．
答案解析收藏纠错 + 选题
23. (2023九下·宿迁开学考) 如图，船A、B在东西方向的海岸线 $\text{[math]}$ 上，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东 $\text{[math]}$ 方向上，在船B的北偏西 $\text{[math]}$ 方向上， $\text{[math]}$ 海里.
1. （1）求船P到海岸线 $\text{[math]}$ 的距离；
2. （2）若船A、船B分别以20海里/时、15海里/时的速度同时出发，匀速直线前往救援，试通过计算判断哪艘船先到达船P处.（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
24. (2023九上·宿城期末) 如图，在正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作：
1. （1）利用网格确定该圆弧所在圆的圆心D点的位置，则D点坐标为；
2. （2）连接AD、CD，则⊙D的半径为(结果保留根号)，∠ADC的度数为；
3. （3）若扇形DAC是一个圆锥的侧面展开图，求该圆锥底面半径.(结果保留根号).
答案解析收藏纠错 + 选题
25. (2023九下·宿迁开学考) 如图，已知△ABC，以AC为直径的 $\text{[math]}$ 交AB于点D，点E为 $\text{[math]}$ 的中点，连接CE交AB于点F，且BF＝BC.
1. （1）判断直线BC与 $\text{[math]}$ 的位置关系，并说明理由；
2. （2）若 $\text{[math]}$ 的半径为2， $\text{[math]}$ ，求CE的长.
答案解析收藏纠错 + 选题
26. (2024九上·宜兴月考) 某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件.
1. （1）写出商场销售这种文具，每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式.
2. （2）若商场要每天获得销售利润2000元，销售单价应定为多少元？
3. （3）求销售单价为多少元时，该文具每天的销售利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
27. (2023九下·宿迁开学考) 如图，抛物线y＝ax ²＋bx＋c（a≠0）的顶点坐标为（2，－1），并且与y轴交于点C（0，3），与x轴交于两点A，B.
1. （1）求抛物线的表达式；
2. （2）设抛物线的对称轴与直线BC交于点D，连接AC、AD，求△ACD的面积；
3. （3）点E为直线BC上一动点，过点E作y轴的平行线EF，与抛物线交于点F.问是否存在点E，使得以D、E、F为顶点的三角形与△BCO相似.若存在，求出点E的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
28. (2023九下·宿迁开学考)

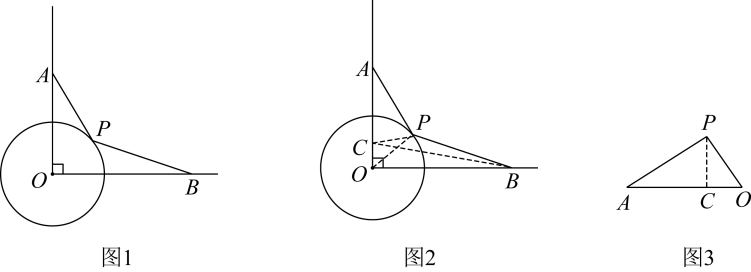
【问题呈现】如图1，∠AOB=90°， OA=4，OB=5，点P在半径为2的⊙O上，求 $\text{[math]}$ 的最小值.

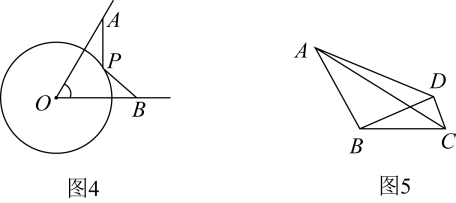
【问题解决】小明是这样做的：如图2，在OA上取一点C使得OC=1，这样可得 $\text{[math]}$ ，又因为∠COP=∠POA，所以可得△COP ∽△POA，所以 $\text{[math]}$ ，得 $\text{[math]}$ 所以 $\text{[math]}$ .

又因为 $\text{[math]}$ ，所以 $\text{[math]}$ 最小值为 ▲ .

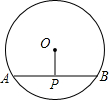
【思路点拨】小明通过构造相似形（图3），将 $\text{[math]}$ 转化成CP，再利用“两点之间线段”最短”求出CP+ BP的最小值.

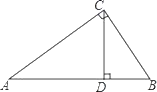
【尝试应用】如图4，∠AOB=60°， OA=10，OB=9，点P是半径为6的⊙O上一动点，求 $\text{[math]}$ 的最小值.

【能力提升】如图5，∠ABC=120°， BA= BC=8，点D为平面内一点且BD= 3CD，连接AD，则△ABD面积的最大值为 ▲ .

答案解析收藏纠错 + 选题