
 C .
C .  D .
D . 编织数量/个 | 2 | 3 | 4 | 5 | 6 |
人数/人 | 3 | 6 | 5 | 4 | 2 |
请根据上表,判断下列说法正确的是( )
V(单位: | 1 | 1.5 | 2 | 2.5 | 3 |
P(单位: | 96 | 64 | 48 | 38.4 | 32 |
P与V的函数关系可能是( )
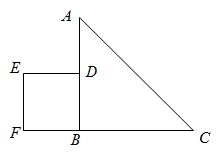
 B .
B .  C .
C .  D .
D . 

(结果精确到 , 参考数据:
)
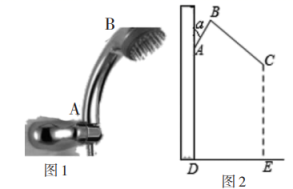
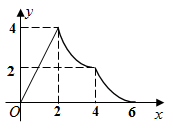
①当时,直接写出区域W内的整点个数;
②若区域W内恰有2个整点,结合函数图象,求k的取值范围.
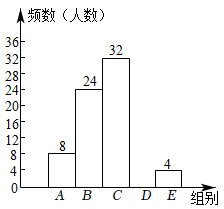
组别 | 学习时间x(h) | 频数(人数) |
A | 8 | |
B | 24 | |
C | 32 | |
D | n | |
E | 4小时以上 | 4 |

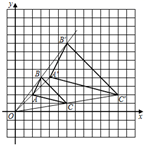
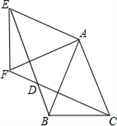
如图1,在四边形中,点P为
上一点,当
时,求证:
.
若将角改为锐角(如图2),其他条件不变,上述结论还成立吗?说明理由.
如图3,在中,
,
, 以点A为直角顶点作等腰
. 点D在
上,点E在
上,点F在
上,且
, 若
, 求
的长.