
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
参与志愿者活动的时间(h) | 1 | 2 | 3 | ||
参与志愿者活动的人数(人) | x | 8 | 2 |
根据表中数据,下列说法中错误的是( )

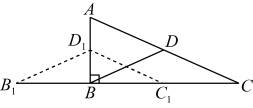
 B .
B . 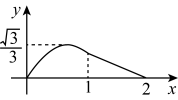 C .
C .  D .
D . 
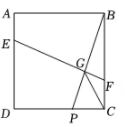
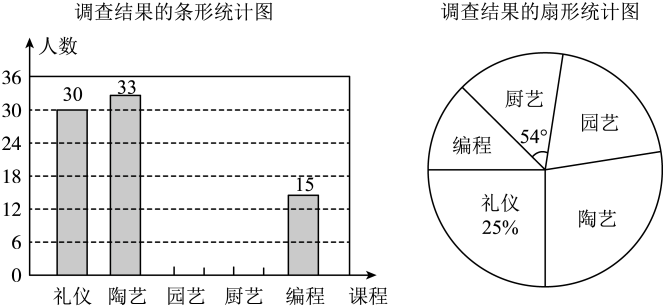
请结合上述信息,解答下列问题:
销售单价x(元) | 40 | 50 |
月销售量y(件) | 100 | 80 |
