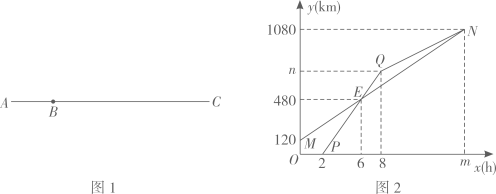
B .
B .  C .
C .  D .
D . 
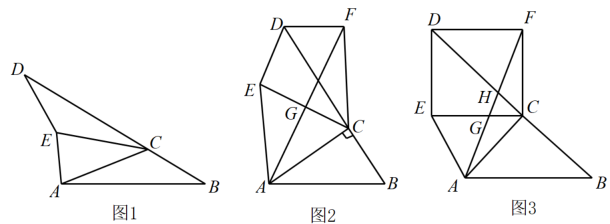
 B .
B .  C .
C . 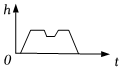 D .
D . 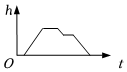
支撑物高度h(cm) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
小车下滑时间t(s) | 4.23 | 3.00 | 2.45 | 2.13 | 1.89 | 1.71 | 1.59 |
根据表格所提供的信息,下列说法中错误的是( )
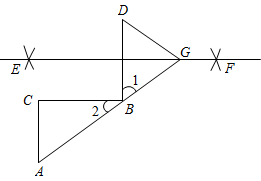
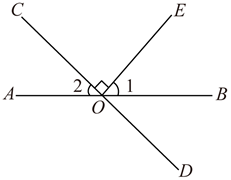
∵(已知)
∴∠DBC= ▲ (垂直的定义)
∵(已知)
∴∠DBC= ▲ (等量代换)
∴ ▲ ( )
∴∠1= ▲ ( )
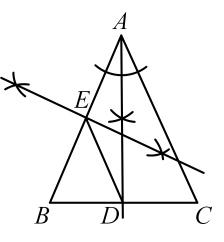
由作图法可知:直线EF是线段DB的 ▲
∴GD= ▲ (线段垂直平分线上的点到这条线段两个端点的距离相等)
∴∠1=∠D(等腰三角形的两个底角相等)
∴∠A=∠D(等量代换)
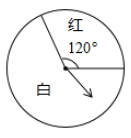
①若事件A为必然事件,则m的值为;
②若事件A为随机事件,则m的值为.
∴ ▲ ⊥BC,BE⊥AC,
∴ ▲ °,
∴ ,
,
▲
,
∴ ,
∵∠ABC=45°,
∴ ▲ ,
∴ ,
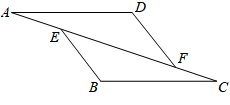
∵在△FDB和△CDA中 , ∴
;
∴ ▲ ,
∴ ,
∴ ▲
,
∴FA=FG,
∴ ▲ + ▲
.