
 B .
B .  C .
C .  D .
D . 
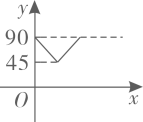 B .
B . 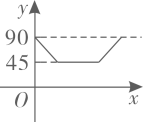 C .
C . 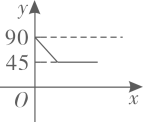 D .
D . 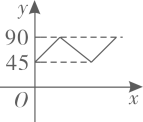


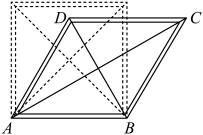


(参考数据:sin37°≈ ,cos37°≈
,tan37°≈
,tan84°≈
)

根据图中信息,解答下列问题:
|
类别价格 |
A款玉带石 |
B款玉带石 |
|
进货价(元/个) |
40 |
30 |
|
销售价(元/个) |
56 |
45 |



