 B .
B .  C .
C . 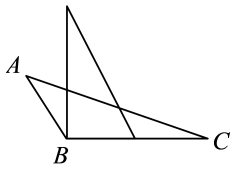 D .
D . 

 B .
B .  C .
C .  D .
D . 
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线 , 则直线a与c平行.

|
|
0 |
2 |
4 |
6 |
8 |
10 |
|
h/厘米 |
30 |
29 |
28 |
27 |
26 |
25 |
试说明 . 请完善解答过程,并在括号内填写相应的理论依据.

解:∵ , (已知)
∴∠1=∠ =60°.( )
∵∠1=∠C,(已知)
∴∠C=∠B=60°.(等量代换)
∵ , (已知)
∴∠C+∠ =180°.( )
∴∠ =180°-∠C=180°-60°=120°.(等式的性质)
∵DE平分∠ADC,(已知)
∴∠ADE=∠ADC=
×120°=60°.( )
∴∠1=∠ADE.(等量代换)
∴ . ( )

例如,把二次三项式进行配方
解:
我们定义:一个整数能表示成(a,b是整数)的形式,则称这个数为“完美数”例如,5是“完美数”,理由:因为
, 再如,
, (x,y是整数)所以M也是“完美数”
下列各数中,“完美数”有.(填序号)
①10 ②45 ③28 ④29
已知(x,y是整数,k是常数),要使S为“完美数”,试求出符合条件的k的值.
已知实数x,y满足 , 求
的最小值.
课外数学兴趣小组活动时,老师提出了如下何题:
如图①,中,若
,
, 求
边上的中线
的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长至点E,使
, 连接
, 请根据小明的方法思考:

解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
如图②,是
的中线,
交
于E,交
于F,且
. 若
,
, 求线段
的长.
如图③,在中,D为
的中点,
分别交
于点E,F.求证:
.