浙江省温州市2023年中考数学试卷

更新时间：2023-06-26 浏览次数：654 类型：中考真卷

一、选择题（本题有10小题，第1-5小题，每小题3分，第6-10小题，每小题4分，共35分。每小题只有一个选项是正确的，不选、多选、错选，均不给分）

1. 如图，比数轴上点 $\text{[math]}$ 表示的数大3的数是（）

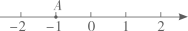
A . -1 B . 0 C . 1 D . 2

答案解析收藏纠错 + 选题
2. 截面为扇环的几何体与长方体组成的摆件如图所示，它的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
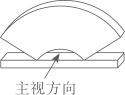
3. (2024七上·伊春期中) 苏步青来自“数学家之乡”，为纪念其卓越贡献，国际上将一颗距地球约218000000公里的行星命名为“苏步青星”.数据218000000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·温州) 阅读背景素材，完成下面小题.
某校计划组织研学活动，现有四个地点可供选择：南麂岛、百丈漈、楠溪江、雁荡山.
1. （1）若从中随机选择一个地点，则选中“南麂岛”或“百丈漈”的概率为（）
  
  A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$
2. （2）为了解学生想法，校方进行问卷调查（每人选一个地点），并绘制成如图所示统计图.已知选择雁荡山的有270人，那么选择楠溪江的有（）
  
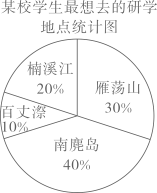
  A . 90人 B . 180人 C . 270人 D . 360人
答案解析收藏纠错 + 选题
5. (2023·温州) 化简 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·从江模拟) 一瓶牛奶的营养成分中，碳水化合物含量是蛋白质的1.5倍，碳水化合物、蛋白质与脂肪的含量共30g.设蛋白质、脂肪的含量分别为 $\text{[math]}$ ，可列出方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
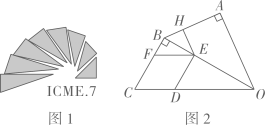
7. (2024·叙永模拟) 图1是第七届国际数学教育大会（ICME）的会徽，图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF，使点D，E，F分别在边OC，OB，BC上，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ .当 $\text{[math]}$ $\text{[math]}$ 时，EH的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. 如图，四边形ABCD内接于 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数与BC的长分别为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·温州) 【素材1】某景区游览路线及方向如图所示，①④⑥各路段路程相等，⑤⑦⑧各路段路程相等，②③两路段路程相等.

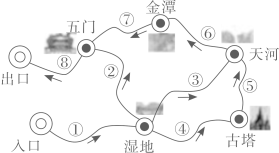
【素材2】设游玩行走速度恒定，经过每个景点都停留20分钟.小温游路线①④⑤⑥⑦⑧用时3小时25分钟；小州游路线①②⑧，他离入口的路程 $\text{[math]}$ 与时间 $\text{[math]}$ 的关系（部分数据）如图所示，在2100米处，他到出口还要走10分钟.

【问题】路线①③⑥⑦⑧各路段路程之和为（）

A . 4200米 B . 4800米 C . 5200米 D . 5400米

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，第11-15小题，每小题4分，第16小题5分，共25分）

10. (2024·邹平模拟) 分解因式： $\text{[math]}$ 。

答案解析收藏纠错 + 选题
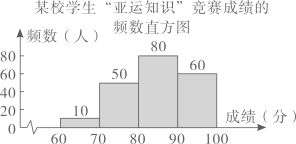
11. 某校学生“亚运知识”竞赛成绩的频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，其中成绩在80分及以上的学生有人.

答案解析收藏纠错 + 选题
12. (2024·长沙模拟) 不等式组 $\text{[math]}$ 的解是。

答案解析收藏纠错 + 选题
13. (2024九下·哈尔滨模拟) 若扇形的圆心角为 $\text{[math]}$ ，半径为18，则它的弧长为。

答案解析收藏纠错 + 选题
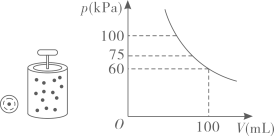
14. (2023·温州) 在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对气缸壁所产生的压强 $\text{[math]}$ 与气缸内气体的体积 $\text{[math]}$ 成反比例， $\text{[math]}$ 关于 $\text{[math]}$ 的函数图象如图所示.若压强由 $\text{[math]}$ 加压到 $\text{[math]}$ ，则气体体积压缩了 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2023·温州) 图1是 $\text{[math]}$ 方格绘成的七巧板图案，每个小方格的边长为 $\text{[math]}$ ，现将它前拼成一个“房子”造型（如图2），过左侧的三个端点作圆，并在圆内右侧部分留出矩形CDEF作为题字区域（点A，E，D，B在圆上，点C，F在AB上），形成一幅装饰画，则圆的半径为.若点A，N，M在同一直线上， $\text{[math]}$ ，则题字区域的面积为.

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，共90分.解答需写出必要的文字说明、演算步骤或证明过程）

16. (2023·温州) 计算：
1. （1） $\text{[math]}$ .
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
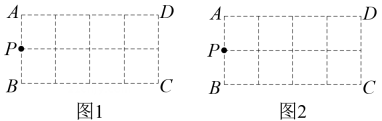
17. (2023·温州) 如图，在 $\text{[math]}$ 的方格纸ABCD中，每个小方格的边长为1.已知格点 $\text{[math]}$ ，请按要求画格点三角形（顶点均在格点上）.
1. （1）在图1中画一个等腰三角形PEF，使底边长为 $\text{[math]}$ ，点 $\text{[math]}$ 在BC上，点 $\text{[math]}$ 在AD上，再画出该三角形绕矩形ABCD的中心旋转 $\text{[math]}$ 后的图形.
2. （2）在图2中画一个Rt $\text{[math]}$ ，使 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在AD上，再画出该三角形向右平移1个単位后的图形.
答案解析收藏纠错 + 选题

18. (2023·温州) 某公司有A、B、C三种型号电动汽车出租，每辆车每天费用分别为300元、380元、500元，阳阳打算从该公司租一辆汽车外出旅游一天，往返行程为210km，为了选择合适的型号通过网络调查，获得三种型号汽车充满电后的里程数据如图所示.

型号	平均里程（km）	中位数（km）	众数（km）
B	216	215	220
C	227.5	227.5	225

A，B，C三种型号电动汽车充满电后能行驶里程的统计图

（1）阳阳已经对B，C型号汽车数据统计如下表，请继续求出A型号汽车的平均里程、中位数和众数.
（2）为了尽可能避免行程中充电耽误时间，又能经济实惠地用车，请你从相关统计量和符合行程要求的百分比等进行分析，给出合理的用车型号建议。

答案解析收藏纠错 + 选题

19. 如图，在直角坐标系中，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，过点 $\text{[math]}$ 的直线交 $\text{[math]}$ 轴于点 $\text{[math]}$ .
1. （1）求m的值和直线AB的函数表达式。
2. （2）若点 $\text{[math]}$ 在线段AB上，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题
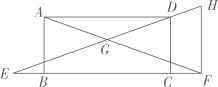
20. (2024·长沙模拟) 如图，已知矩形ABCD，点 $\text{[math]}$ 在CB延长线上，点 $\text{[math]}$ 在BC延长线上，过点 $\text{[math]}$ 作 $\text{[math]}$ 交ED的延长线于点 $\text{[math]}$ ，连结AF交EH于点 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ .
2. （2）当 $\text{[math]}$ 时，求EF的长.
答案解析收藏纠错 + 选题
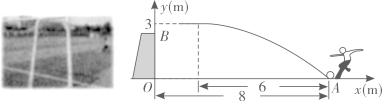
21. (2024·长沙模拟) 一次足球训练中，小明从球门正前方8m的 $\text{[math]}$ 处射门，球射向球门的路线呈抛物线.当球飞行的水平距离为6m时，球达到最高点，此时球离地面3m.已知球门高OB为2.44m，现以 $\text{[math]}$ 为原点建立如图所示直角坐标系.
1. （1）求抛物线的函数表达式，并通过计算判断球能否射进球门（忽略其他因素）。
2. （2）对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则当时他应该带球向正后方移动多少米射门，才能让足球经过点 $\text{[math]}$ 正上方2.25m处?
答案解析收藏纠错 + 选题

22. (2023·温州) 根据背景素材，探索解决问题.

测算发射塔的高度
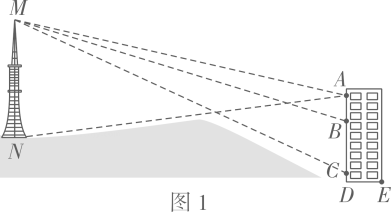
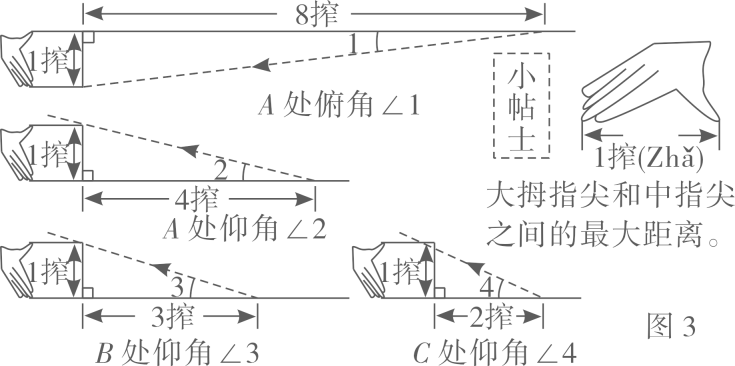
背景素材	某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度MN（如图1）.他们通过自制的测倾仪（如图2）在A，B，C三个位置观测，测倾仪上的示数如图3所示.

	经讨论，只需选择其中两个合适的位置，通过测量﹑换算就能计算发射塔的高度.
问题解决
任务1	分析规划	选择两个观测位置：点 ▲ 和点 ▲ 。
	获取数据	写出所选位置观测角的正切值，并量出观测点之间的图上距离.
任务2	推理计算	计算发射塔的图上高度MN.
任务3	换算高度	楼房实际宽度DE为12米，请通过测量换算发射塔的实际高度.

注：测量时，以答题纸上的图上距离为准，并精确到1mm.

答案解析收藏纠错 + 选题

23. (2024九下·郁南模拟) 如图1，AB为半圆 $\text{[math]}$ 的直径， $\text{[math]}$ 为BA延长线上一点，CD切半圆于点 $\text{[math]}$ ，交CD延长线于点 $\text{[math]}$ ，交半圆于点 $\text{[math]}$ ，已知 $\text{[math]}$ .如图2，连结AF，P为线段AF上一点，过点 $\text{[math]}$ 作BC的平行线分别交CE，BE于点M，N，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ .设 $\text{[math]}$ .
1. （1）求CE的长和 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式.
2. （2）当 $\text{[math]}$ ，且长度分别等于 $\text{[math]}$ ， $\text{[math]}$ 的三条线段组成的三角形与 $\text{[math]}$ 相似时，求 $\text{[math]}$ 的值.
3. （3）延长 $\text{[math]}$ 交半圆 $\text{[math]}$ 于点 $\text{[math]}$ ，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题