山东省青岛市局属学校2023年中考三模数学试题

更新时间：2023-07-20 浏览次数：114 类型：中考模拟

一、单选题

1. (2023七上·淮安期中) 下列四个选项，其中的数不是分数的选项是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·青岛模拟) 下列计算正确的是（）

A . -（2x²）³＝8x⁶ B . x⁵÷x²＝x³ C . 3x²×2x³＝6x⁶ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·青岛模拟) 下面图形中，既是中心对称图形又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023·青岛模拟) 甲、乙两名同学本学期五次引体向上的测试成绩(个数)成绩如图所示，下列判断正确的是( )

A . 甲的成绩比乙稳定 B . 甲的最好成绩比乙高 C . 甲的成绩的平均数比乙大 D . 甲的成绩的中位数比乙大

答案解析收藏纠错 + 选题
5. (2023·青岛模拟) 如图，AB、AC为⊙O的切线，B和C是切点，延长OB到点D，使BD＝OB，连接AD，若∠DAC＝78°，则∠ADO等于（）

A . 70° B . 64° C . 62° D . 51°

答案解析收藏纠错 + 选题
6. (2023·青岛模拟) 如图，将线段AB先绕原点O按逆时针方向旋转90°，再向下平移4个单位，得到线段A'B'，则点B的对应点B'的坐标是（）

A . （－3，－1） B . （－3，－3） C . （－1，－3） D . （－1，－2）

答案解析收藏纠错 + 选题
7. (2023·青岛模拟) 如图．正方形ABCD和正方形CEFG中，点D在CG上， $\text{[math]}$ ， H是AF的中点，CH＝3，那么CE的长是（）

A . 3 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·青岛模拟) 抛物线 $\text{[math]}$ （a，b，c为常数， $\text{[math]}$ ）经过 $\text{[math]}$ ， $\text{[math]}$ 两点．则下列四个结论正确的有（）
① $\text{[math]}$ ；② $\text{[math]}$ ；③若该抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 有交点，则a的取值范围是 $\text{[math]}$ ；④对于a的每一个确定值，如果一元二次方程 $\text{[math]}$ （t为常数， $\text{[math]}$ ）的根为整数，则t的值只有3个．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

9. (2023·青岛模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2023·青岛模拟) 国家卫健委通报：截至2022年6月1日，31个省（自治区、直辖市）和新疆生产建设兵团累计报告接种新冠病毒疫苗101000万余剂次，将数据101000用科学记数法表示为．

答案解析收藏纠错 + 选题
11. (2023·青岛模拟) 某工厂四月份生产口罩50万个，防疫需要，预计第二季度生产182万个口罩的生产任务，该工厂增加设备，并提高生产效率，设该工厂五、六月份生产口罩平均每月的增长率为x，那么x=

答案解析收藏纠错 + 选题
12. (2023·青岛模拟) 如图，在同一平面直角坐标系中，直线 $\text{[math]}$ （t为常数）与反比例函数 $\text{[math]}$ ， $\text{[math]}$ 的图象分别交于点A，B，点O为坐标原点，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
13. (2023·青岛模拟) 如图， $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为直径作半圆，圆心为O．以点C为圆心， $\text{[math]}$ 为半径作弧 $\text{[math]}$ ，过点O作 $\text{[math]}$ 的平行线交两弧于点D、E，则阴影部分的面积是．

答案解析收藏纠错 + 选题
14. (2023·青岛模拟) 如图，正方形 $\text{[math]}$ 的边长为4，延长 $\text{[math]}$ 至E使 $\text{[math]}$ ，以 $\text{[math]}$ 为边在上方作正方形，延长 $\text{[math]}$ 交 $\text{[math]}$ 于M，连接 $\text{[math]}$ ， $\text{[math]}$ ， H为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 分别与 $\text{[math]}$ 、 $\text{[math]}$ 交于点N、K．则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④若点P是 $\text{[math]}$ 上一点，则 $\text{[math]}$ 最小值为 $\text{[math]}$ ．其中正确的结论有．（填序号）

答案解析收藏纠错 + 选题

三、解答题

15. (2023·青岛模拟) 已知： $\text{[math]}$ 求作： $\text{[math]}$ 内的一个最大的菱形，使 $\text{[math]}$ 为菱形的一个内角．

答案解析收藏纠错 + 选题
16. (2023·青岛模拟) 计算
1. （1）化简： $\text{[math]}$ ；
2. （2）解不等式组 $\text{[math]}$ ，并求出不等式组的整数解之和．
答案解析收藏纠错 + 选题
17. (2023·青岛模拟) 4张相同的卡片上分别写有数字0、1、 $\text{[math]}$ 、3，将卡片的背面朝上，洗匀后从中任意抽取1张，将卡片上的数字记录下来；再从余下的3张卡片中任意抽取1张，同样将卡片上的数字记录下来．
1. （1）第一次抽取的卡片上数字是非负数的概率为．
2. （2）小敏设计了如下游戏规则：当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时，甲获胜；否则，乙获胜．小敏设计的游戏规则公平吗？为什么？（请用树状图或列表等方法说明理由）
答案解析收藏纠错 + 选题
18. (2023·青岛模拟) 如图， $\text{[math]}$ 、 $\text{[math]}$ 是两个核酸检测点，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 是附近的在同一条直线上的三个小区的物业服务中心，在 $\text{[math]}$ 处测得点 $\text{[math]}$ 在正北 $\text{[math]}$ 处，点 $\text{[math]}$ 在北偏东 $\text{[math]}$ ，在 $\text{[math]}$ 处测得点 $\text{[math]}$ 在北偏东 $\text{[math]}$ ，点 $\text{[math]}$ 在北偏西 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 、 $\text{[math]}$ 两个小区的物业服务中心距离．
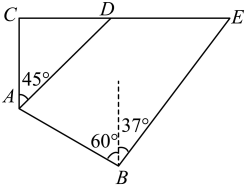
（结果保留整数，参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题

19. (2023·青岛模拟) 某学校开展了主题为“垃圾分类，绿色生活新时尚”的宣传活动.为了解学生对垃圾分类知识的掌握情况，学校从全校学生中随机抽取部分学生进行知识测试（测试满分100分，得分均为整数），并对成绩进行整理、描述和分析.部分信息如下：

a.成绩频数分布表与扇形统计图：

学生测试成绩的频数表

组别	成绩a（分）	频数（人）	各组总分数（分）
A	50≤a＜60	10	552
B	60≤a＜70	15	971
C	70≤a＜80	m	1512
D	80≤a＜90	40	3393
E	90≤a≤100	15	1422

b.成绩在60≤a＜70这一组的是：60 62 64 65 66 66 67 67 67 68 69 65 61 63 67

根据以上信息，回答下列问题：

（1）填空：m＝，n＝，所抽取学生成绩在60≤a＜70这一组的众数是分；
（2）求所抽取学生的平均成绩；
（3）若该校有1400名学生，假设全部参加此次测试，请估计成绩不低于80分的人数.

答案解析收藏纠错 + 选题

20. (2023·青岛模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ ，过点A作 $\text{[math]}$ 交 $\text{[math]}$ 于点D，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 到点E，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 半径的长．
答案解析收藏纠错 + 选题
21. (2023·青岛模拟) 如图，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于A（1，8），B（4，n）两点，与x轴，y轴分别交于点D，C．
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）连接OA，OB，求 $\text{[math]}$ 的面积；
3. （3）将直线 $\text{[math]}$ 向下平移t（ $\text{[math]}$ ）个单位后，与双曲线 $\text{[math]}$ 有唯一交点，直接写出t的值．
答案解析收藏纠错 + 选题
22. (2023·青岛模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点E是边 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ 的延长线与边 $\text{[math]}$ 相交于点F， $\text{[math]}$ ，交 $\text{[math]}$ 于点G，连接 $\text{[math]}$ 、 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）已知（从以下两个条件中选择一个作为已知，填写序号），请判断四边形 $\text{[math]}$ 的形状，并证明你的结论．
  条件①： $\text{[math]}$ ；
  
  条件②： $\text{[math]}$ ．
  
  （注：如果选择条件①条件②分别进行解答，按第一个解答计分）
答案解析收藏纠错 + 选题
23. (2023·青岛模拟) 如图①，有一组平行线l₁∥l₂∥l₃∥l₄ ，正方形ABCD的四个顶点分别在l₁、l₂、l₃、l₄上，EG过点D且垂直于l₁于点E，分别交l₂、l₄于点F、G，EF＝DG＝1，DF＝2.
1. （1） AE＝，正方形ABCD的边长＝；
2. （2）如图②，将∠AED绕点A顺时针旋转α°得到∠AE′D′，且0°＜α＜90°，点D′在直线l₃上，以AD′为边在E′D′左侧作菱形AD′C′B′，使点B′、C′分别在直线l₂、l₄上．
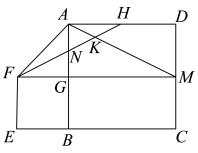
  ①写出∠B′AD′与α的函数关系并给出证明；
  ②若α＝30°，求菱形AD′C′B′的边长．
答案解析收藏纠错 + 选题
24. (2024九下·越秀模拟) 某商店为了推销一种新产品，在某地先后举行40场产品发布会，已知该产品每台成本为10万元，设第x场产品的销售量为y（台），已知第一场销售产品49台，然后每增加一场，产品就少卖出1台；
1. （1）直接写出y与x之间满足的函数关系式；产品的每场销售单价p（万元）由基本价和浮动价两部分相加组成，其中基本价保持不变，经过统计，发现第1场—第20场浮动价与发布场次x成正比，第21场—第40场浮动价与发布场次x成反比，得到如下数据：
  x（场）
  3
  10
  25
  p（万元）
  10.6
  12
  14.2
2. （2）求p与x之间满足的函数关系式；
3. （3）当产品销售单价为13万元时，求销售场次是第几场？
4. （4）在这40场产品发布会中，求哪一场获得的利润最大，最大利润是多少？
答案解析收藏纠错 + 选题
25. (2023·青岛模拟) 如图①，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ cm， $\text{[math]}$ cm， $\text{[math]}$ cm，动点M在 $\text{[math]}$ 上运动，从C点出发到B点，速度每秒2cm；动点N在 $\text{[math]}$ 上运动，从B点出发到A点，速度每秒1cm，两个动点同时出发，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t（秒）．
1. （1）当 $\text{[math]}$ 时，求t的值？
2. （2）设三角形 $\text{[math]}$ 的面积为S，求S与t之间的函数关系式；
3. （3）如图②，连接 $\text{[math]}$ ，是否存在某一时刻t，使 $\text{[math]}$ 与 $\text{[math]}$ 互相垂直？若存在，求t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题