 B .
B .  C .
C .  D .
D . 
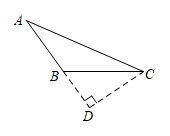 B .
B . 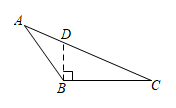 C .
C .  D .
D . 
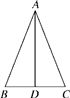

|
时间x/年 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
2022 |
|
常住人口y/千万人 |
|
|
|
|
|
|
|
请你根据表格回答下列问题:

解:因为与
是同样大小的含30°角的直角三角形(已知),
所以 ,
,
▲
,
所以 ,
所以(等量代换),
即平分
( ),
在与
中,
因为 ,
( ),
(已知),
所以( ),
所以 ▲ ,
所以是等腰三角形(等腰三角形的定义),
又因为F是的中点,
所以 ▲ (等腰三角形“三线合一”),
因为 ,
所以 ,
又因为 ,
,
,
所以 ▲ (角平分线上的点到这个角两边的距离相等).