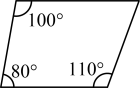
 B .
B .  C .
C . 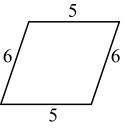 D .
D . 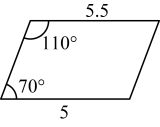
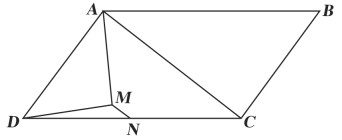
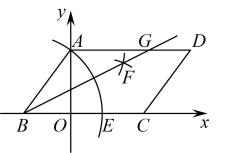
已知:如图,
求证: | |
方法一 证明:如图,延长
| 方法二 证明:如图,过点A作
|
①当旋转角为时,在方格中画出
;
②旋转中,当最长时,求
的坐标.
(一)用配方法因式分解: .
解:原式
(二)用配方法求代数式的最小值.
解:原式
∵ , ∴
, ∴
的最小值为
.
若实数a,b满足 , 则
的最小值为.