2023-2024学年初中数学七年级上册 3.2 代数式同...

更新时间：2023-08-19 浏览次数：45 类型：同步测试

一、选择题

1. (2023·包河模拟) 随着国产芯片自主研发的突破，某种型号芯片的价格经过两次降价，由原来每片a元下降到每片b元，已知第一次下降了 $\text{[math]}$ ，第二次下降了20%，则a与b满足的数量关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七下·卢龙期末) 某商场促销，小明将促销信息告诉了妈妈，现假设某一商品的定价为x元，小明妈妈根据信息列出了不等式 $\text{[math]}$ ，那么小明告诉妈妈的信息是（）

A . 买两件等值的商品可减150元，再打八折，最后不超过1500元 B . 买两件等值的商品可打八折，再减150元，最后不超过1500元 C . 买两件等值的商品可减150元，再打八折，最后不到1500元 D . 买两件等值的商品可打八折，再减150元，最后不到1500元

答案解析收藏纠错 + 选题
3. (2023七下·海淀期末) 张师傅下岗再就业，做超了小商品生意，某次进货时，他以每件a元的价格购进了20件甲种小商品，每件b元的价格购进了30件乙种小商品（ $\text{[math]}$ ）回来后，根据市场行情，他将这两种小商品都以每件 $\text{[math]}$ 元的价格出售，在这次买卖中，张师傅是（）

A . 赔钱 B . 赚钱 C . 不赚不赔 D . 无法确定赚和赔

答案解析收藏纠错 + 选题
4. (2022七上·杨浦期中) 如图，正方形 $\text{[math]}$ 与正方形 $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，已知正方形 $\text{[math]}$ 的边长 $\text{[math]}$ ，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ，用 $\text{[math]}$ 、 $\text{[math]}$ 表示下列面积， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，下列各选项中错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·宁波模拟) 如图，大矩形分割成五个小矩形，④号、⑤号均为正方形，其中⑤号正方形边长为1．若②号矩形的长与宽的差为2，则知道哪个小矩形的周长，就一定能算出这个大矩形的面积（）

A . ①或③ B . ② C . ④ D . 以上选项都可以

答案解析收藏纠错 + 选题
6. (2023·合肥模拟) 已知我省2022年上半年的 $\text{[math]}$ 总值为 $\text{[math]}$ 万亿元，2022年下半年的 $\text{[math]}$ 总值比2022年上半年增长 $\text{[math]}$ ，预计2023年上半年的 $\text{[math]}$ 总值比2022年下半年增长 $\text{[math]}$ ，若预计我省2023年上半年的 $\text{[math]}$ 总值为 $\text{[math]}$ 万亿元，则a，b之间的关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023七上·桂平期末) 【阅读理解】计算：25×11＝275，13×11＝143，48×11＝528，74×11＝814，观察算式，我们发现两位乘11的速算方法：头尾一拉，中间相加，满十进一.
【拓展应用】已知一个两位数，十位上的数字是a，个位上的数字是b，这个两位数乘11，计算结果的十位上的数字可表示为（　　）

A . a或a＋1 B . a＋b或ab C . a＋b−10 D . a＋b或a＋b−10

答案解析收藏纠错 + 选题
8. (2021七上·镇海期中) 如图所示的大长方形被分割成4个大小不同的正方形(1)(2)(4)和一个小长方形(5)，有下列结论：
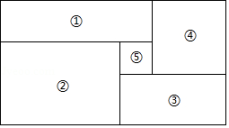
（ 1 ）若已知小正方形(1)和(2)的周长，就能求出大长方形的周长；（2）若已知小正方形(3)的周长，就能求出大长方形的周长；（3）若已知小正方形(4)的周长，就能求出大长方形的周长；(4) 若已知小长方形(5)的周长，就能求出大长方形的周长。其中正确的是（）

A . (1) (2) (4) B . (1) (2) (3) C . (1) (3) D . (2) (3)

答案解析收藏纠错 + 选题

二、填空题

9. 2023长春马拉松于5月21日在南岭体育场鸣枪开跑，某同学参加了7.5公里健康跑项目，他从起点开始以平均每分钟x公里的速度跑了10分钟，此时他离健康跑终点的路程为公里．（用含x的代数式表示）

答案解析收藏纠错 + 选题
10. (2021七上·瑞安月考) 如图所示，已知长方形ABCD的长AD=8，内有边长相等的小正方形AIGJ和小正方形ELCK，其重叠部分为长方形EFGH．设小正方形边长为a，则EH的长为(用a的代数式表示)．若长方形ABCD的宽AB=6，长方形EFGH的周长为8，则图中阴影部分周长和为．

答案解析收藏纠错 + 选题
11. (2023七下·顺德期中) 任意给一个非零数 $\text{[math]}$ ，按下列程序写出输出结果：（写出 $\text{[math]}$ 与 $\text{[math]}$ 的关系式）．

答案解析收藏纠错 + 选题
12. (2023七上·金华月考) 有一个长方体水箱，从里面量得它的深度为 $\text{[math]}$ ，底面长为 $\text{[math]}$ ，宽为 $\text{[math]}$ ，水箱里已盛有深度为 $\text{[math]}$ 的水.若往水箱里放入一个棱长为 $\text{[math]}$ 的立方体铁块，则水箱的水深为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2021七上·诸暨期中) 如图，把六张形状大小完全相同的小长方形卡片（如图①）不重叠的放在一个底面为长方形（长为acm，宽为bcm）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是.

答案解析收藏纠错 + 选题

三、解答题

14. (2022七下·浙江) 底面为正方形的长方体，体积为 $\text{[math]}$ ，底面边长为 $\text{[math]}$ ，请用含 $\text{[math]}$ 的式子表示这个长方体的高 $\text{[math]}$ ，并求当底面边长为 $\text{[math]}$ 时 $\text{[math]}$ 的值.

答案解析收藏纠错 + 选题
15. (2022七上·易县期中) 某建筑物的窗户如图所示，它的上部是由4个扇形组成的半圆形，下部是由边长都为 $\text{[math]}$ 的4个小正方形组成的正方形，用含 $\text{[math]}$ 的代数式表示制造窗框的材料总长（即图中所有黑线的长度和）．

答案解析收藏纠错 + 选题

四、综合题

16. (2022七上·大田期中) 如图
1. （1）【操作感知】如图①，长方形透明纸上有一条数轴， $\text{[math]}$ 是周长为4的圆的直径，点 $\text{[math]}$ 与数轴原点重合，将圆从原点出发沿数轴正方向滚动1周，点 $\text{[math]}$ 落在数轴上的点 $\text{[math]}$ 处；将圆从原点出发沿数轴负方向滚动半周，点 $\text{[math]}$ 落在数轴上的点 $\text{[math]}$ 处，折叠长方形透明纸，使数轴上的点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，此时折痕与数轴交点表示的数为.
2. （2）【建立模型】折叠长方形透明纸，使得数轴上表示数 $\text{[math]}$ 的点 $\text{[math]}$ 与表示数 $\text{[math]}$ 的点 $\text{[math]}$ 重合，则折痕与数轴交点表示的数为（用含 $\text{[math]}$ ， $\text{[math]}$ 的代数式表示）.
3. （3）【问题解决】若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为数轴上不同的三点，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数为-2，如果 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点中的一点到其余两点的距离相等，求点 $\text{[math]}$ 表示的数；
4. （4）如图②，若 $\text{[math]}$ 是周长为 $\text{[math]}$ 的圆的直径，点 $\text{[math]}$ 与数轴原点重合，将圆从原点出发沿数轴正方向滚动2周，点 $\text{[math]}$ 落在数轴上的点 $\text{[math]}$ 处；将圆从原点出发沿数轴负方向滚动 $\text{[math]}$ 周，点 $\text{[math]}$ 落在数轴上的点 $\text{[math]}$ 处.将此长方形透明纸沿 $\text{[math]}$ ， $\text{[math]}$ 剪开，将点 $\text{[math]}$ ， $\text{[math]}$ 之间一段透明纸对折，使其左、右两端重合，这样连续对折 $\text{[math]}$ 次后，再将其展开，求最右端折痕与数轴交点表示的数.
答案解析收藏纠错 + 选题
17. (2022七上·奉贤期中) 阅读以下材料，并解答问题．
阅读一：画与三角形面积相等的长方形．
1. （1）如图1，已知 $\text{[math]}$ ， ①画 $\text{[math]}$ 边上的高 $\text{[math]}$ ；②取线段 $\text{[math]}$ 的中点E；③以 $\text{[math]}$ 为边画长方形 $\text{[math]}$ ，使得 $\text{[math]}$ 那么长方形 $\text{[math]}$ 的面积等于 $\text{[math]}$ 的面积．
  根据“阅读一”，如果 $\text{[math]}$ ，那么长方形 $\text{[math]}$ 的面积= ▲ ．
  阅读二：画与长方形面积相等的正方形．
  如图2，已知长方形 $\text{[math]}$ ， ①延长 $\text{[math]}$ ，截取 $\text{[math]}$ ；
  ②以 $\text{[math]}$ 的中点O为圆心， $\text{[math]}$ 为半径作半圆；
  ③过点F画 $\text{[math]}$ 的垂线，交半圆于点I；④以 $\text{[math]}$ 为边画正方形 $\text{[math]}$ 那么正方形 $\text{[math]}$ 的面积等于长方形 $\text{[math]}$ 的面积．
2. （2）根据“阅读二”，设 $\text{[math]}$ ，如果等面积的正方形 $\text{[math]}$ 边长为5，请猜想a、b的数量关系并加以说明；
3. （3）根据“阅读一”由 $\text{[math]}$ 画出它的等面积长方形 $\text{[math]}$ ，在长方形 $\text{[math]}$ 的基础上，再根据“阅读二”画出等面积正方形FIJK，设 $\text{[math]}$ ，当H为 $\text{[math]}$ 的中点时，m、n的数量关系为：．
答案解析收藏纠错 + 选题