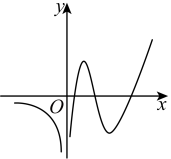
 B .
B . 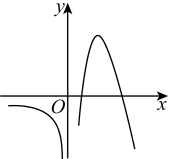 C .
C .  D .
D . 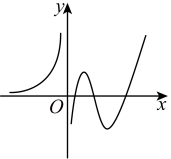

参考数据:当
认为两个变量间的相关性较强
参考公式相关系数
,
回归方程中的斜率和截距的最小二乘法估计公式分别为
,
.
附: , 其中
.
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
|
|
感兴趣 |
不感兴趣 |
合计 |
|
男生 |
12 |
||
|
女生 |
5 |
||
|
合计 |
30 |
①求实数的取值范围;
②求证:.