2023-2024学年初中数学九年级上册 25.7 相似多边...

更新时间：2023-09-09 浏览次数：29 类型：同步测试

一、选择题

1. (2023·鲁甸模拟) 如图，小明在边长均为1的正方形网格中，分别作了 $\text{[math]}$ 和 $\text{[math]}$ ，其中 $\text{[math]}$ 三个顶点坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 和 $\text{[math]}$ 是以原点 $\text{[math]}$ 为位似中心的位似图形，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·舟山模拟) 在平面直角坐标系中，已知点 $\text{[math]}$ ，以原点O为位似中心，相似比为 $\text{[math]}$ ，把 $\text{[math]}$ 缩小，则点A的对应点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·高明模拟) 如图， $\text{[math]}$ 与 $\text{[math]}$ 位似，位似中心为点 $\text{[math]}$ .若 $\text{[math]}$ 的周长与 $\text{[math]}$ 的周长比为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·德城模拟) 如图，△AOC中三个顶点的坐标分别为（4，0）、（0，0）、（4，3），AP为△AOC中线，以O为位似中心，把△AOP每条边扩大到原来的2倍，得到 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·青海模拟) 每年秋季开学，学校组织同学们进行视力测试，如图是视力表的一部分，其中开口向上的两个“ $\text{[math]}$ ”之间的变换是（）

A . 平移 B . 对称 C . 位似 D . 旋转

答案解析收藏纠错 + 选题
6. (2023·舒城模拟) 将一张 $\text{[math]}$ （ $\text{[math]}$ ）纸片，以它的一边为边长剪去一个菱形，将余下的平行四边形中，再以它的一边为边长剪去一个菱形，若剪去两个菱形后所剩下的平行四边形与原来 $\text{[math]}$ 相似，则 $\text{[math]}$ 的相邻两边 $\text{[math]}$ 与 $\text{[math]}$ 的比值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·鄞州期末) 如图，E，F，G，H分别是矩形 $\text{[math]}$ 四条边上的点，连接 $\text{[math]}$ 相交于点I，且 $\text{[math]}$ ， $\text{[math]}$ ，矩形 $\text{[math]}$ 矩形 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点P，Q，下列一定能求出 $\text{[math]}$ 面积的条件是（）

A . 矩形 $\text{[math]}$ 和矩形 $\text{[math]}$ 的面积之差 B . 矩形 $\text{[math]}$ 与矩形 $\text{[math]}$ 的面积之差 C . 矩形 $\text{[math]}$ 和矩形 $\text{[math]}$ 的面积之差 D . 矩形 $\text{[math]}$ 和矩形 $\text{[math]}$ 的面积之差

答案解析收藏纠错 + 选题
8. (2022九上·镇海区期中) 如图，点P是平行四边形 $\text{[math]}$ 内部一点，过P分别作 $\text{[math]}$ 和 $\text{[math]}$ 的平行线交平行四边形 $\text{[math]}$ 的四边于 $\text{[math]}$ . 连结 $\text{[math]}$ 分别交 $\text{[math]}$ 于M和N. 若四边形 $\text{[math]}$ 四边形 $\text{[math]}$ ，且四边形 $\text{[math]}$ 的面积是四边形 $\text{[math]}$ 的3倍. 下列选项正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2023八下·深圳期末) 如图，在平面直角坐标系中，已知A(1，0)，B(2，1)，D(3，0)，△ABC与△DEF位似，原点O是位似中心，则E点的坐标是.

答案解析收藏纠错 + 选题
10. (2023八下·肇源月考) 一个六边形六边长分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，另一个与它相似的六边形的最短边为 $\text{[math]}$ ，则其周长为．

答案解析收藏纠错 + 选题
11. (2023·浙江模拟) 如图，△OAB与△OCD是以点O为位似中心的位似图形，位似比为1∶2，∠OCD=90°，CO=CD=2，则点B的坐标为．

答案解析收藏纠错 + 选题
12. (2021九上·椒江期末) 如图，把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的 L 型放入矩形 ABCD 中.矩形Ⅰ的一个顶点落在 L 型中正方形的顶点 E 处，其他顶点在矩形 ABCD 的边上； L 型中的正方形有三个顶点恰好在矩形 ABCD 的边上，另有一个顶点和小正方形顶点合.若矩形Ⅰ与矩形 ABCD相似，则 AB：BC 的值为.

答案解析收藏纠错 + 选题
13. (2021九上·德惠期末) 如图，在平面直角坐标系中，等边△ABC与等边△BDE是以原点为位似中心的位似图形，且相似比为 $\text{[math]}$ ，点A、B、D在x轴上，若等边△BDE的边长为6，则点C的坐标为．

答案解析收藏纠错 + 选题

三、解答题

14. (2022八下·龙口期末) 如图，△ABC的三个顶点的坐标分别为A（3，1），B（1，2），C（4，3）．以原点O为位似中心，在第一象限内将△ABC放大为原来的2倍得到△A₁B₁C₁ ，作出△A₁B₁C₁ ，并写出A₁ ， B₁ ， C₁的坐标；

答案解析收藏纠错 + 选题
15. (2021九上·吉林期末) 放缩尺是一种绘图工具，它能把图形放大或缩小．
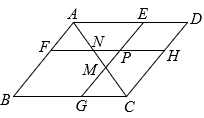
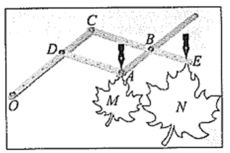
制作：把钻有若干等距小孔的四根直尺用螺栓分别在点A，B，C，D处连接起来，使得直尺可以绕着这些点转动，O为固定点， $\text{[math]}$ ， $\text{[math]}$ ，在点A，E处分别装上画笔．
画图：现有一图形M，画图时固定点O，控制点A处的笔尖沿图形M的轮廓线移动，此时点E处的画笔便画出了将图形M放大后的图形N．
原理：
连接 $\text{[math]}$ ， $\text{[math]}$ ，可证得以下结论：
① $\text{[math]}$ 和 $\text{[math]}$ 为等腰三角形，则 $\text{[math]}$ ， $\text{[math]}$ （180°-∠            ▲             ）；
②四边形 $\text{[math]}$ 为平行四边形（理由是            ▲            ）；
③ $\text{[math]}$ ，于是可得O，A，E三点在一条直线上；
④当 $\text{[math]}$ 时，图形N是以点O为位似中心，把图形M放大为原来的            ▲            倍得到的．

答案解析收藏纠错 + 选题

四、综合题

16. (2021·鼓楼模拟) 学完“探索三角形相似的条件”之后，小明所在的学习小组尝试探索四边形相似的条件，以下是他们的思考，请你和他们一起完成探究过程.
（定义）四边成比例，且四角分别相等的两个四边形叫做相似四边形.
1. （1）（初步思考）
  小明根据探索三角形相似的条件所获得的经验，考虑可以从定义出发逐步弱化条件探究四边形相似的条件.他考虑到“四角分别相等的两个四边形相似”可以举出反例“矩形”，“四边成比例的两个四边形相似”可以举出反例.所以四边形相似的条件必须再添加条件，于是，可以从“四边成比例，且一角对应相等的两个四边形相似”，“三边成比例，且两角分别相等的两个四边形相似”，“两边成比例，且三角分别相等的两个四边形相似”来探究.
2. （2）（深入探究）
  学习小组一致认为，“四边成比例，且一角对应相等的两个四边形相似”是真命题，请结合图形完成证明.
  
  已知：四边形 $\text{[math]}$ 和四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .
  
  求证：四边形 $\text{[math]}$ 四边形 $\text{[math]}$ .证明：
3. （3）对于“三边成比例，且两角分别相等的两个四边形相似”，学习小组得到如下的四个命题：
  ①“三边成比例，两邻角分别相等且只有一角为其中两边的夹角的两个四边形相似”；
  
  ②“三边成比例，两邻角分别相等且都不是其中两边的夹角的两个四边形相似”；
  
  ③“三边成比例及其两夹角分别相等的两个四边形相似”；
  
  ④“三边成比例，两对角分别相等的两个四边形相似”.
  
  其中真命题是.（填写所有真命题的序号）
4. （4）请你完成“两边成比例，且三角分别相等的两个四边形相似”的探究过程.
答案解析收藏纠错 + 选题