 B .
B .  C .
C . 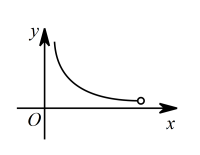 D .
D . 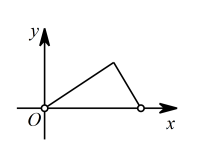

|
A.14% |
B.11% |
C.10% |
D.9% |
②若2014年城镇居民人均可支配收入按①中的年平均增长率增长,请预测2014年的城镇居民人均可支配收入为万元(结果精确到0.1).

①在点、
、
中,点
的“等距点”是;
②若点在直线
上,且
、
两点为“等距点”,则点
的坐标为;
①若、
是直线
上的两点,且
、
为“等距点”,求
的值;
②当时,半径为
的
上存在一点
, 线段
上存在一点
, 使得
、
两点为“等距点”,直接写出
的取值范围.