

 B .
B .  C .
C .  D .
D . 


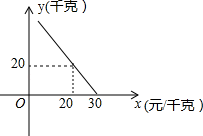



某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,喷出的水柱形状可以看作是抛物线的一部分.若记水柱上某一位置与水管的水平距离为米,与湖面的垂直高度为
米.下面的表中记录了
与
的五组数据:
| 0 | 1 | 2 | 3 | 4 |
| 0.5 | 1.25 | 1.5 | 1.25 | 0.5 |

①此抛物线的函数表达式为 ▲ . (函数表达式用一般式表示)
②按规定,车顶部与隧道顶部在竖直方向上的高度差至少0.5米,则此隧道限高 ▲ 米.
③已知人行道台阶高均为0.3米,按照国家标准,人行道宽度不得低于1.25米,该隧道的人行道宽度设计是否达标?说明理由.
+


乒乓球到球台的竖直高度记为(单位:
),乒乓球运行的水平距离记为
(单位:
).测得如下数据:
|
水平距离x/ |
|
|
|
|
|
|
|
|
竖直高度y/ |
|
|
|
|
|
|
|

②求满足条件的抛物线解析式;
现剩余100盒食品需要处理,经过降价处理后还是无法销售的只能积压在仓库,损失本金,若使亏损金额最小,此时每盒食品的售价应为元;