一、选择题(本大题共9小题,共27.0分。在每小题列出的选项中,选出符合题目的一项)
-
-
-
A . 2
B . 3
C . 3.5
D . 5
-
-
-
-
-
A .  B . 2
C . 4
D .
B . 2
C . 4
D . 
-
二、多选题(本大题共1小题,共3.0分。在每小题有多项符合题目要求)
-
10.
(2023九上·黄埔开学考)
如图,正方形

的顶点

,

别在

轴、

轴上,

,

, 若

的中点

恰好落在

轴上,此时

恰好也垂直于

轴,

交

轴于点

, 连接

判断:

;

是等边三角形;

;

其中正确的有( )

三、填空题(本大题共6小题,共18.0分)
-
11.
(2023九上·黄埔开学考)
在甲、乙两位射击运动员的10次考核成绩中,两人的考核成绩的平均数相同, 方差分别为

,

, 则考核成绩更为稳定的运动员是
(填“甲”、“乙”中的一个)
-
-
-
-
-
四、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
-
(1)
计算:

;
-
(2)
解方程:

.
-
-
-
20.
(2023九上·黄埔开学考)
某中学为了解初三学生参加志愿者活动的次数,随机调查了该年级20名学生,统计得到该20名学生参加志愿者活动的次数如下:3;5;3;6;3;4;4;5;2;4;5;6;1;3;5;5;4;4;2;4
根据以上数据,得到如下不完整的频数分布表:
|
次数
|
1
|
2
|
3
|
4
|
5
|
6
|
|
人数
|
1
|
2
|
a
|
6
|
b
|
2
|
-
(1)
表格中的

,

;
-
(2)
在这次调查中,参加志愿者活动的次数的众数为,中位数为;
-
(3)
若该校初三年级共有300名学生,根据调查统计结果,估计该校初三年级学生参加志愿者活动的次数为4次的人数.
-
-
(1)
求点

的坐标;
-
(2)
点

是

轴上一点,且

的面积为4,求直线

的解析式.
-
22.
(2023九上·黄埔开学考)
“地摊经济”已成为社会关注的热门话题,小明从市场得知如下信息:
|
|
甲商品
|
乙商品
|
|
进价(元/件)
|
65
|
5
|
|
售价(元/件)
|
90
|
10
|
小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
-
-
(2)
小明用不超过3500元资金一次性购进甲、乙两种商品,求x的取值范围;
-
(3)
在(2)的条件下,若要求甲、乙商品全部销售完后获得的利润不少于1250元,请说明当x为何值时利润最大,最大利润是多少?
-
-
(1)
尺规作图:作

的平分线
AF , 交
CD于点
F , 连结
EF、
BF(保留作图痕迹,不写作法);
-
(2)
在(1)所作的图中,若

,且

,证明:

为等边三角形.
-
-
(1)
当点

运动到

中点时,证明:四边形

是平行四边形;
-
(2)
当

时,求

的长.
-
-
(1)
求出直线

的解析式;
-
(2)
若动点

从点

出发,沿线段

以每分钟

个单位的速度运动,过

作

交

轴于

, 连接

设运动时间为

分钟,当四边形

为平行四边形时,求

的值.
-
(3)

为直线

上一点,在坐标平面内是否存在一点

使得以

、 、

、

为顶点的四边形为菱形?若存在,求出此时

的坐标;若不存在请说明理由.

 B .
B .  C .
C . 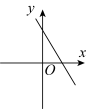 D .
D .