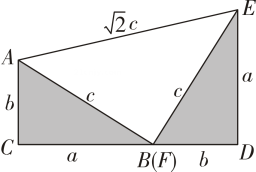
 B .
B .  C .
C . 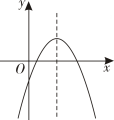 D .
D . 
|
x |
-3 |
0 |
2 |
|
y |
-6 |
6 |
4 |
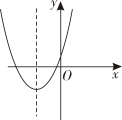
下面有四个结论:
①该二次函数的图象经过点;
②当时,该二次的数有最大值为
;
③若和
都在该二次函数的图象上,则
;
④将该二次函数图象向左平移个单位长度后得到函数图象的顶点在y轴上.
其中正确的结论有( )

请阅读下列材料,完成后面的任务:
一元二次方程根的两个性质及其应用
我们知道,一元二次方程的求根公式是
, 由公式可知,一元二次方程的根是由它的系数决定的,即它的根与系数有着密切的关系,那么一元二次方程的根与系数有何关系?下面介绍一元二次方程的两个根与系数关系的另外两个性质(非根与系数的关系定理,即非韦达定理):
性质1:在一元二次方程中,若
(即各项的系数和为0),则一元二次方程
的两个根分别是
,
. 下面我们给出它的证明过程:
证明:∵ , ∴
,
∴ ,
∴ ,
.
性质2:在一元二次方程中,若
, 则一元二次方程
的两个根分别是
,
.
证明:…….
任务:
.
;
.
;
.
;
.
.
【项目学习】
配方法是数学中重要的一种思想方法,利用配方法可求一元二次方程的根,也可以求二次函数的顶点坐标等.所谓配方法是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法.其实这种方法还经常被用到代数式的变形中,并结合非负数的意义解决某些问题.
例1:把代数式进行配方.
解:原式 .
例2:求代数式的最大值.
解:原式 .
,
,
,
的最大值为
.
【问题解决】