江苏省苏州市常熟市2023-2024学年高二上册数学暑期调查...

更新时间：2023-11-16 浏览次数：31 类型：开学考试

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1. (2023高二上·常熟开学考) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023高二上·常熟开学考) 已知命题 $\text{[math]}$ ： $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的否定是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023高二上·常熟开学考) 在空间中， $\text{[math]}$ ， $\text{[math]}$ 是不重合的直线， $\text{[math]}$ ， $\text{[math]}$ 是不重合的平面，则下列说法正确的是（）

A . 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023高二上·常熟开学考) 函数 $\text{[math]}$ 在 $\text{[math]}$ 的图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023高二上·常熟开学考) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的中点，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023高二上·常熟开学考) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023高二上·常熟开学考) 古代数学家刘徽编撰的 $\text{[math]}$ 重差 $\text{[math]}$ 是中国最早的一部测量学著作，也为地图学提供了数学基础 $\text{[math]}$ 现根据刘徽的 $\text{[math]}$ 重差 $\text{[math]}$ 测量一个球体建筑物的高度，已知点 $\text{[math]}$ 是球体建筑物与水平地面的接触点 $\text{[math]}$ 切点 $\text{[math]}$ ，地面上 $\text{[math]}$ ， $\text{[math]}$ 两点与点 $\text{[math]}$ 在同一条直线上，且在点 $\text{[math]}$ 的同侧 $\text{[math]}$ 若在 $\text{[math]}$ ， $\text{[math]}$ 处分别测得球体建筑物的最大仰角为 $\text{[math]}$ 和 $\text{[math]}$ ，且 $\text{[math]}$ ，则该球体建筑物的高度约为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高二上·常熟开学考) 在四面体 $\text{[math]}$ 中，已知二面角 $\text{[math]}$ 为直二面角， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ 若满足条件的四面体 $\text{[math]}$ 有两个，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题（本大题共4小题，共20.0分。在每小题有多项符合题目要求）

9. (2023高二上·常熟开学考) 已知 $\text{[math]}$ 为虚数单位，以下四个说法中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 若 $\text{[math]}$ ，则复数 $\text{[math]}$ 对应的点位于第四象限 D . 已知复数 $\text{[math]}$ 满足： $\text{[math]}$ ，则 $\text{[math]}$ 在复平面内对应的点的轨迹为圆

答案解析收藏纠错 + 选题
10. (2023高二上·常熟开学考) 袋子中有5个大小质地完全相同的球，分别标有数字1，2，3，4，5，从中有放回地依次随机摸出2个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第一次取出的球的数字是偶数”，丙表示事件“两次取出的球的数字都是偶数”，丁表示事件“两次取出的球的数字之和为6”，则（）

A . 甲与乙是对立事件 B . 甲与乙是互斥事件 C . 丙与丁相互独立 D . 甲与丁相互独立

答案解析收藏纠错 + 选题
11. (2023高二上·常熟开学考) 若定义在 $\text{[math]}$ 上的奇函数 $\text{[math]}$ 满足 $\text{[math]}$ ，且当 $\text{[math]}$ 时， $\text{[math]}$ ，则（）

A . $\text{[math]}$ 为偶函数 B . $\text{[math]}$ 在 $\text{[math]}$ 上单调递增 C . $\text{[math]}$ 在 $\text{[math]}$ 上单调递增 D . $\text{[math]}$ 的最小正周期 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023高二上·常熟开学考) 如图，若正方体 $\text{[math]}$ 的棱长为 $\text{[math]}$ ，点 $\text{[math]}$ 是正方体在侧面 $\text{[math]}$ 上的一个动点 $\text{[math]}$ 含边界 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，则下列结论正确的是（）

A . 三棱锥 $\text{[math]}$ 的体积为定值 B . 四棱锥 $\text{[math]}$ 外接球的半径为 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为 $\text{[math]}$ D . 若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题（本大题共4小题，共20.0分）

13. (2023高二上·常熟开学考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023高二上·常熟开学考) 若圆锥侧面展开图是圆心角为 $\text{[math]}$ ，半径为 $\text{[math]}$ 的扇形，则这个圆锥表面积为．

答案解析收藏纠错 + 选题
15. (2023高二上·常熟开学考) 请写出一个定义域不是 $\text{[math]}$ ，但值域为 $\text{[math]}$ 的奇函数： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2023高二上·常熟开学考) 在锐角三角形ABC中，已知 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 的最小值是.

答案解析收藏纠错 + 选题

四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

17. (2023高二上·常熟开学考) 已知复数 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 在复平面内的对应点位于第二象限，求 $\text{[math]}$ 的取值范围；
2. （2）若 $\text{[math]}$ 为纯虚数，设 $\text{[math]}$ ， $\text{[math]}$ 在复平面上对应的点分别为 $\text{[math]}$ ， $\text{[math]}$ ，求向量 $\text{[math]}$ 在向量 $\text{[math]}$ 上的投影向量的坐标．
答案解析收藏纠错 + 选题
18. (2023高二上·常熟开学考) 某企业为了深入学习贯彻党的二十大精神，组织全体 $\text{[math]}$ 位党员开展“学习二十大，争当领学人”党史知识竞赛，所有党员的成绩均在 $\text{[math]}$ 内，成绩分成 $\text{[math]}$ 组，按照下面分组进行统计分析：第 $\text{[math]}$ 组 $\text{[math]}$ ，第 $\text{[math]}$ 组 $\text{[math]}$ ，第 $\text{[math]}$ 组 $\text{[math]}$ ，第 $\text{[math]}$ 组 $\text{[math]}$ ，第 $\text{[math]}$ 组 $\text{[math]}$ ，并绘制成频率分布直方图如图所示，按比例分配的分层抽样的方法在第 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 组共选取 $\text{[math]}$ 人作为企业“二十大精神”的宣传使者．
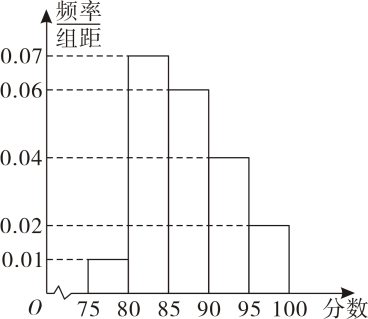
1. （1）根据频率分布直方图，估计党员成绩的样本数据的第 $\text{[math]}$ 百分位数；
2. （2）若从 $\text{[math]}$ 位宣传使者中随机选取两人参加宣传活动，求第 $\text{[math]}$ 组中至多有一人被选中的概率．
答案解析收藏纠错 + 选题
19. (2023高二上·常熟开学考) 已知函数 $\text{[math]}$ 为奇函数，且 $\text{[math]}$ 图象的相邻两对称轴间的距离为 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的解析式及单调减区间；
2. （2）将函数 $\text{[math]}$ 的图象向右平移 $\text{[math]}$ 个单位长度，再把横坐标缩小为原来的 $\text{[math]}$ 纵坐标不变 $\text{[math]}$ ，得到函数 $\text{[math]}$ 的图象，当 $\text{[math]}$ 时，求方程 $\text{[math]}$ 的所有根之和．
答案解析收藏纠错 + 选题
20. (2023高二上·常熟开学考) 记 $\text{[math]}$ 的内角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，已知 $\text{[math]}$ 面积为 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，且 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ ， $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2023高二上·常熟开学考) 如图，在四棱锥 $\text{[math]}$ 中， $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）已知 $\text{[math]}$ 为线段 $\text{[math]}$ 上一点，若 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正切值为 $\text{[math]}$ ，试确定 $\text{[math]}$ 点位置；并求此时二面角 $\text{[math]}$ 的大小．
答案解析收藏纠错 + 选题
22. (2023高二上·常熟开学考) 已知函数 $\text{[math]}$ 过定点 $\text{[math]}$ ，且点 $\text{[math]}$ 在函数 $\text{[math]}$ 的图象上， $\text{[math]}$ ．
1. （1）求函数 $\text{[math]}$ 的解析式；
2. （2）若定义在区间 $\text{[math]}$ 上的函数 $\text{[math]}$ 有零点，求整数 $\text{[math]}$ 的值；
3. （3）设 $\text{[math]}$ ，若对于任意 $\text{[math]}$ ，都有 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题