吉林省松原市乾安县2023-2024学年九年级上学期期中数学...

更新时间：2023-11-27 浏览次数：33 类型：期中考试

一、选择题（本大题共6小题，每小题2分，共12分）

1. (2023九上·乾安期中) 一元二次方程 $\text{[math]}$ 的二次项系数、一次项系数、常数项分别是（）

A . 4，6，1 B . 4，6， $\text{[math]}$ C . 4， $\text{[math]}$ ， 1 D . 4， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·乾安期中) 中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九上·北京市期中) 若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个相等的实数根，则实数 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 9

答案解析收藏纠错 + 选题
4. (2023九上·曾都期中) 已知二次函数 $\text{[math]}$ ，下列说法正确的是（）

A . 对称轴为 $\text{[math]}$ B . 顶点坐标为 $\text{[math]}$ C . 函数的最大值是 $\text{[math]}$ D . 函数的最小值是 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·乾安期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 A 顺时针旋转 $\text{[math]}$ 、C 旋转后的对应点分别是 $\text{[math]}$ 和 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·乾安期中) 如图，抛物线 $\text{[math]}$ 经过正方形 $\text{[math]}$ 的三个顶点A，B，C，点B在 $\text{[math]}$ 轴上，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共8小题，每小题3分，共24分）

7. (2024·修水模拟) 已知关于x的方程 $\text{[math]}$ 的一个根是 $\text{[math]}$ ，则它的另一个根是．

答案解析收藏纠错 + 选题
8. (2023九上·乾安期中) 已知一元二次方程 $\text{[math]}$ 有两个实数根 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值等于．

答案解析收藏纠错 + 选题
9. 将抛物线 $\text{[math]}$ 向下平移1个单位长度，再向右平移个单位长度后，得到的新抛物线经过原点．

答案解析收藏纠错 + 选题
10. 如图，一名学生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $\text{[math]}$ ，则铅球推出的距离 $\text{[math]}$ m．

答案解析收藏纠错 + 选题
11. (2023九上·乾安期中) 在方格纸上建立如图所示的平面直角坐标系，将 $\text{[math]}$ 绕点O按顺时针方向旋转 $\text{[math]}$ ，得 $\text{[math]}$ ，则点A的对应点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
12. (2023九上·乾安期中) 我们古代数学家研究过一元二次方程．下面是我国南宋数学家杨辉在1275年提出的一个问题：“直田积（矩形面积）八百六十四步（平方步），只云阔（宽）不及长一十二步（宽比长少一十二步），问阔及长各几步．”意思是一块田是矩形，矩形面积为 $\text{[math]}$ ，长比宽多 $\text{[math]}$ ，如果设宽为 $\text{[math]}$ ，则列出的方程为．

答案解析收藏纠错 + 选题
13. (2024九上·襄州期末) 如图，将面积为7的正方形 $\text{[math]}$ 和面积为9的正方形 $\text{[math]}$ 分别绕原点O顺时针旋转，使 $\text{[math]}$ ， $\text{[math]}$ 落在数轴上，点A，D在数轴上对应的数字分别为a，b，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023九上·乾安期中) 如图，二次函数 $\text{[math]}$ 图像的一部分与x轴的一个交点坐标为 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ，结合图像给出下列结论：
① $\text{[math]}$ ；
② $\text{[math]}$ ；
③ $\text{[math]}$ ；
④关于x的一元二次方程 $\text{[math]}$ 有两个不相等的实数根；
⑤若点 $\text{[math]}$ ， $\text{[math]}$ 均在该二次函数图象上，则 $\text{[math]}$ ．其中正确结论的序号为．

答案解析收藏纠错 + 选题

三、解答题（每小题5分，共20分）

15. (2024九下·青秀开学考) 解方程： $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2023九上·乾安期中) 在平面直角坐标系xOy中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ，求抛物线的表达式．

答案解析收藏纠错 + 选题
17. (2023九上·乾安期中) 如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A逆时针旋转至 $\text{[math]}$ 处，使点B落在BC延长线上的D点处，求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
18. (2023九上·乾安期中) 为增强学生身体素质，某校开展篮球比赛，赛制为单循环形式（每两队之间赛一场）．现计划安排21场比赛，应安排多少个球队参赛．

答案解析收藏纠错 + 选题

四、解答题（每小题7分，共28分）

19. (2023九上·乾安期中) 如图，在建立平面直角坐标系的网格纸中，每个小方格都是边长为1个单位长度的小正方形， $\text{[math]}$ 的顶点均在格点上，点P的坐标为 $\text{[math]}$ ．
⑴把 $\text{[math]}$ 绕点P旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，作出 $\text{[math]}$ ；
⑵把 $\text{[math]}$ 向右平移7个单位长度得到 $\text{[math]}$ ，作出 $\text{[math]}$ ；
⑶ $\text{[math]}$ 与 $\text{[math]}$ 是否成中心对称？若是，则找出对称中心 $\text{[math]}$ ，并写出其坐标；若不是，请说明理由．

答案解析收藏纠错 + 选题
20. 已知关于x的一元二次方程 $\text{[math]}$ ．
1. （1）求证：无论m取何值时，方程都有两个不相等的实数根；
2. （2）设该方程的两个实数根为a，b，若 $\text{[math]}$ ，求m的值．
答案解析收藏纠错 + 选题
21. (2023九上·乾安期中) 如图，点 $\text{[math]}$ 是等边三角形 $\text{[math]}$ 内的一点， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 按顺时针旋转得到 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 。
1. （1）求 $\text{[math]}$ 的度数；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长。
答案解析收藏纠错 + 选题
22. (2023九上·乾安期中) 超市的某种牛奶平均每天可销售20箱，每箱盈利30元．为了尽快减少库存，商场决定采取适当的降价措施．经调查发现，若每箱降价1元，每天可多售5箱，若设每箱降价x元．
1. （1）根据题意，填表：
  
  每箱利润（元）
  销售量（箱）
  利润（元）
  降价前
  30
  20
  600
  降价后
  ①
  ②
2. （2）若每天盈利1200元，则每箱应降价多少元？
答案解析收藏纠错 + 选题

五、解答题（每小题8分，共16分）

23. (2023九上·乾安期中) 在杭州举行的亚运会比赛中，一名运动员在 $\text{[math]}$ 高的跳台进行跳水，身体（看成一点）在空中的运动轨迹是一条抛物线，运动员离水面OB的高度 $\text{[math]}$ 与离起跳点A的水平距离 $\text{[math]}$ 之间的函数关系如图所示，运动员离起跳点A的水平距离为 $\text{[math]}$ 时达到最高点，当运动员离起跳点A的水平距离为 $\text{[math]}$ 时离水面的距离为 $\text{[math]}$ ．
1. （1）求y关于x的函数表达式；
2. （2）求运动员从起跳点到入水点的水平距离OB的长．
答案解析收藏纠错 + 选题
24. (2023九上·乾安期中) 阅读材料：解方程 $\text{[math]}$ ，我们可以将 $\text{[math]}$ 视为一个整体，然后设 $\text{[math]}$ ，则 $\text{[math]}$ ，原方程化为 $\text{[math]}$ ，解得 $\text{[math]}$ ， $\text{[math]}$ ．
当 $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
当 $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
$\text{[math]}$ 原方程的解为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
根据上面的解答，解决下面的问题：
1. （1）填空：在由原方程得到方程①的过程中，利用法达到降次的目的，体现了的数学思想；
2. （2）解方程 $\text{[math]}$ ．
答案解析收藏纠错 + 选题

六、解答题（每小题10分，共20分）

25. (2023九上·乾安期中) 我们可以通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．
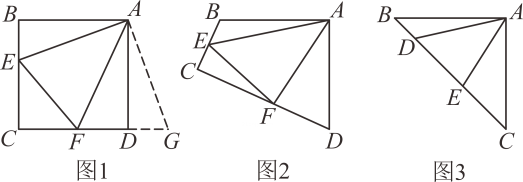
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上， $\text{[math]}$ ，连接EF ，则 $\text{[math]}$ ，试说明理由．
1. （1）思路梳理
  $\text{[math]}$ ，
  $\text{[math]}$ 把 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 至 $\text{[math]}$ ，可使AB与AD重合．
  $\text{[math]}$ ，
  $\text{[math]}$ ，点F、D、G共线．
  根据，易证 $\text{[math]}$ ，得 $\text{[math]}$ ．
2. （2）类比引申
  如图2，四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，点E、F分别在边BC、CD上， $\text{[math]}$ ，若 $\text{[math]}$ 、 $\text{[math]}$ 都不是直角，则当 $\text{[math]}$ 与 $\text{[math]}$ 满足等量关系时，仍有 $\text{[math]}$ ．
3. （3）联想拓展
  如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D、E均在边BC上，且 $\text{[math]}$ ．猜想BD、DE、EC应满足的等量关系，并写出推理过程．
答案解析收藏纠错 + 选题

26. (2023九上·乾安期中) 根据以下素材，探索完成任务．

如何设计拱桥景观灯的悬挂方案？
素材1	图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽 $\text{[math]}$ ，拱顶离水面 $\text{[math]}$ ．据调查，该河段水位在此基础上再涨 $\text{[math]}$ 达到最高．		图1 图2
素材2	为迎佳节，拟在图1桥洞前面的桥拱上悬挂 $\text{[math]}$ 长的灯笼，如图3．为了安全，灯笼底部距离水面不小于 $\text{[math]}$ ；为了实效，相邻两盏灯笼悬挂点的水平间距均为 $\text{[math]}$ ；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．		图3
问题解决
任务1	确定桥拱形状	在图2中建立合适的直角坐标系，求抛物线的函数表达式．
任务2	探究悬挂范围	在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围．
任务3	拟定设计方案（填空即可）	给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标．