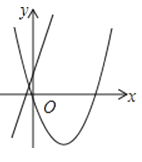
 B .
B . 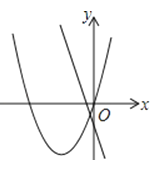 C .
C . 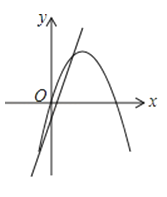 D .
D . 
①例:解方程 .
解:当时,原方程可化为
.
解得: ,
不合题意,舍去
当时,原方程可化为
.
解得: ,
不合题意,舍去
原方程的解是
,
.
问题:已知方程 , 求一个一元二次方程,使它的根分别是已知方程根的
倍.
解:设所求方程的根为 , 则
, 所以,把
代入已知方程,得
;
化简,得;故所求方程为
.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程要求:把所求方程化为一般形式
;