题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

北京市通州区2023-2024学年九年级上学期数学期中考试试...

更新时间：2023-12-24 浏览次数：53 类型：期中考试

一、选择题（本题共8个小题，每小题2分，共16分）每题均有四个选项，符合题意的选项只有一个.

1. (2023九上·通州期中) 下列长度的四条线段中，是成比例线段的是（）

A . 3cm，5cm，6cm，9cm B . 3cm，5cm，8cm，9cm C . 3cm，9cm，10cm，30cm D . 3cm，6cm，7cm，9cm

答案解析收藏纠错 + 选题
2. (2023九上·通州期中) 抛物线 $\text{[math]}$ 的顶点坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·通州期中) 如图所示，点D、E分别在 $\text{[math]}$ 的AB ， AC边上，且 $\text{[math]}$ ，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·通州期中) 将抛物线 $\text{[math]}$ 向下平移3个单位，得到的抛物线为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·通州期中) 如图，图1是可折叠的熨衣架的实物图，图2是它的侧面示意图，AD与CB相交于点O ， $\text{[math]}$ ，根据图2中的数据可得x的值为（）
图1 图2

A . 0.4 B . 0.8 C . 1 D . 1.6

答案解析收藏纠错 + 选题
6. (2023九上·通州期中) 如图，已知D是 $\text{[math]}$ 的边AC上一点，根据下列条件，不能判定 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·莲池模拟) 若二次函数 $\text{[math]}$ 的图象与x轴有公共点，那么m的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
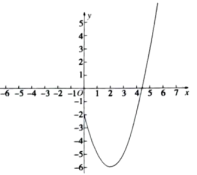
8. (2023九上·通州期中) 函数 $\text{[math]}$ 的自变量x的取值范围为全体实数，其中 $\text{[math]}$ 部分的图象如图所示，对于此函数有下列结论：
①函数图象关于y轴对称
②函数既有最大值，也有最小值
③当 $\text{[math]}$ 时，y随x的增大而减小
④当 $\text{[math]}$ 时，关于x的方程 $\text{[math]}$ 有4个实数根
其中正确的结论个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题（本题共8个小题，每小题2分，共16分）

9. (2023九上·通州期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2023九上·通州期中) 请写出一个开口向下，图象经过原点的二次函数表达式.

答案解析收藏纠错 + 选题
11. (2023九上·通州期中) 两个相似三角形的相似比为2：3，则它们的面积之比为

答案解析收藏纠错 + 选题
12. (2023九上·通州期中) 20世纪70年代初，我国著名的数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果.如图，利用黄金分割法，所做EF将矩形窗框ABCD分为上下两部分，其中E为边AB的黄金分割点， $\text{[math]}$ .已知AB为2米，则线段BE的长为米.

答案解析收藏纠错 + 选题
13. (2023九上·通州期中) 如图，抛物线 $\text{[math]}$ 的对称轴为 $\text{[math]}$ ，点P ，点Q是抛物线与x轴的两个交点，若点P的坐标为 $\text{[math]}$ ，则点Q的坐标为.

答案解析收藏纠错 + 选题
14. (2023九上·通州期中) 点 $\text{[math]}$ ， $\text{[math]}$ 为抛物线 $\text{[math]}$ 上两点，则 $\text{[math]}$ $\text{[math]}$ .（用“＜”或“＞”号连接）

答案解析收藏纠错 + 选题
15. (2023九上·通州期中) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则CD的长为.

答案解析收藏纠错 + 选题
16. (2023九上·通州期中) 如图，在平面直角坐标系中，矩形 $\text{[math]}$ 的边 $\text{[math]}$ 分别在x轴、y轴的正半轴上，点A的坐标为 $\text{[math]}$ ，点P在矩形 $\text{[math]}$ 的内部，点E在 $\text{[math]}$ 边上，且满足 $\text{[math]}$ ，当△ $\text{[math]}$ 是等腰三角形时，点P的坐标为．

答案解析收藏纠错 + 选题

三、解答题（本题共68分，第17-18题每题4分；第19-21题每题5分；第22-27题每题6分；第28题9分）解答应写出文字说明、演算步骤或证明过程.

17. (2023九上·通州期中) 已知一条抛物线的顶点坐标为 $\text{[math]}$ ，且经过点 $\text{[math]}$ ，求抛物线的表达式.

答案解析收藏纠错 + 选题
18. (2023九上·通州期中) 如图， $\text{[math]}$ 的高AD ， BE相交于点O.
1. （1）写出一个与 $\text{[math]}$ 相似的三角形（不添加其他线段），这个三角形是；
2. （2）证明：
答案解析收藏纠错 + 选题
19. (2023九上·通州期中) 已知抛物线 $\text{[math]}$ .
1. （1）求抛物线的顶点坐标及与坐标轴的交点坐标；
2. （2）在平面直角坐标系xOy中画出函数图象.
答案解析收藏纠错 + 选题
20. (2023九上·通州期中) 小华同学用自制的直角三角形纸板DEF测量树的高度AB ，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上.已知纸板的两条直角边 $\text{[math]}$ ， $\text{[math]}$ ，测得边DF离地面的高度 $\text{[math]}$ ， $\text{[math]}$ ，求树的高度.

答案解析收藏纠错 + 选题
21. (2023九上·通州期中) 如图，在矩形ABCD中，E是边AB的中点，连接DE交对角线AC于点F.
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求CF的长.
答案解析收藏纠错 + 选题
22. (2023九上·通州期中) 已知二次函数 $\text{[math]}$ 在 $\text{[math]}$ 和 $\text{[math]}$ 时的函数值相等.
1. （1）求二次函数 $\text{[math]}$ 图象的对称轴；
2. （2）过 $\text{[math]}$ 作x轴的平行线与二次函数 $\text{[math]}$ 的图象交于不同的两点M、N.当 $\text{[math]}$ 时，求b的值.
答案解析收藏纠错 + 选题
23. (2023九上·通州期中) 已知：如图， $\text{[math]}$ 中，AD平分 $\text{[math]}$ ， E是AD上一点，且 $\text{[math]}$ .判断BE与BD的数量关系并证明.

答案解析收藏纠错 + 选题
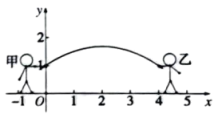
24. (2024八下·丰城期中) 跳绳是大家喜爱的一项体育运动，当绳子甩到最高处时，其形状视为抛物线.如图是甲，乙两人将绳子甩到最高处时的示意图，已知两人拿绳子的手离地面的高度都为1m，并且相距4m，现以两人的站立点所在的直线为x轴，过甲拿绳子的手作x轴的垂线为y轴，建立如图所示的平面直角坐标系，且绳子所对应的抛物线表达式为 $\text{[math]}$ .
1. （1）求绳子所对应的抛物线表达式；
2. （2）身高1.70m的小明，能否站在绳子的正下方，让绳子通过他的头顶？
答案解析收藏纠错 + 选题
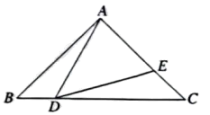
25. (2023九上·通州期中) 如图，在等腰三角形ABC中， $\text{[math]}$ ， $\text{[math]}$ ， D是BC边上的一个动点（不与B、C重合），在AC上取一点E ，使 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）设 $\text{[math]}$ ， $\text{[math]}$ ，求y关于x的函数表达式，并写出自变量x的取值范围.
答案解析收藏纠错 + 选题
26. (2023九上·通州期中) 某水果经销商以每公斤8元的价格购进一批葡萄，若按每公斤20元的价格销售，平均每天可售出60公斤.结合销售记录发现，若售价每降低1元，平均每天的销售量增加10公斤，为了尽快减少库存，该水果商决定降价销售.
1. （1）若每公斤降价2元，则每天的销售利润为元；
2. （2）销售单价定为每公斤多少元时，每天销售该品种葡萄获得的利润w最大？最大利润是多少元？
答案解析收藏纠错 + 选题
27. (2023九上·通州期中) 已知抛物线 $\text{[math]}$ .
1. （1）求抛物线的顶点坐标（用含a的代数式表示）；
2. （2）点 $\text{[math]}$ ， $\text{[math]}$ 在该抛物线上，若 $\text{[math]}$ ，求a的取值范围.
答案解析收藏纠错 + 选题
28. (2023九上·通州期中) 定义：两个相似三角形共边且位于一个角的平分线两侧，则称这样的两个相似三角形为叠似三角形.
图1 图2 图3
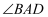
1. （1）如图1，四边形ABCD中，对角线AC平分 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ 和 $\text{[math]}$ 为叠似三角形；
2. （2）如图2， $\text{[math]}$ 和 $\text{[math]}$ 为叠似三角形，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求四边形ABCD的周长；
3. （3）如图3，在 $\text{[math]}$ 中，D是BC上一点，连结AD ，点E在AD上，且 $\text{[math]}$ ， F为AC中点，且 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题

试卷信息