广东省深圳市名校联考2023-2024学年高二上学期数学期中...

更新时间：2024-01-09 浏览次数：37 类型：期中考试

一、单项选择题（每小题只有一个答案符合题意，共8小题，每小题5分，共40分）

1. (2024高二下·成都月考) 在等差数列 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 4 B . 5 C . 6 D . 8

答案解析收藏纠错 + 选题
2. (2023高二上·深圳期中) 在等比数列 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的公比 $\text{[math]}$ （）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
3. (2023高二上·深圳期中) 已知两条直线 $\text{[math]}$ ： $\text{[math]}$ 和 $\text{[math]}$ ： $\text{[math]}$ 相互垂直，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
4. (2023高二上·深圳期中) 已知椭圆C的一个焦点为 $\text{[math]}$ ，且过点 $\text{[math]}$ ，则椭圆C的标准方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023高二上·深圳期中) 在等比数列 $\text{[math]}$ 中， $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的前6项和为（）

A . 22 B . 24 C . 21 D . 27

答案解析收藏纠错 + 选题
6. (2023高二上·深圳期中) 已知F是双曲线C： $\text{[math]}$ 的一个焦点，点P在C的渐近线上，O是坐标原点， $\text{[math]}$ ，则△OPF的面积为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023高二上·深圳期中) 已知椭圆C： $\text{[math]}$ （ $\text{[math]}$ ）的左、右焦点分别为 $\text{[math]}$ 、 $\text{[math]}$ ，若椭圆C上存在一点P ，使得 $\text{[math]}$ 的内切圆的半径为 $\text{[math]}$ ，则椭圆C的离心率的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高二上·深圳期中) 已知双曲线 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，若 $\text{[math]}$ 上的任意一点 $\text{[math]}$ 都满足 $\text{[math]}$ ，则 $\text{[math]}$ 的离心率取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题（共4小题，每小题均有多个选项符合题意，全对得5分，错选得0分，漏选得2分，共20分）

9. (2023高二上·深圳期中) 已知等差数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高二上·深圳期中) 已知圆M： $\text{[math]}$ ，则下列说法正确的是（）

A . 点 $\text{[math]}$ 在随M内 B . 圆M关于 $\text{[math]}$ 对称 C . 半径为 $\text{[math]}$ D . 直线 $\text{[math]}$ 与圆M相切

答案解析收藏纠错 + 选题
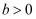
11. (2023高二上·深圳期中) 已知双曲线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的右焦点为F ，过点F且斜率为k（ $\text{[math]}$ ）的直线l交双曲线于A、B两点，线段AB的中垂线交x轴于点D ．若 $\text{[math]}$ ，则双曲线的离心率的值可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023高二上·深圳期中) 若数列 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ ），则称该数列为斐波那契数列．如图所示的“黄金螺旋线”是根据斐波那契数列画出来的曲线．图中的长方形由以斐波那契数为边长的正方形拼接而成，在每个正方形中作圆心角为90°的扇形，连接起来的曲线就是“黄金螺旋线”．记以 $\text{[math]}$ 为边长的正方形中的扇形面积为 $\text{[math]}$ ，数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ．则下列说法正确的是（）：

A . $\text{[math]}$ B . $\text{[math]}$ 是奇数 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题（共4小题，每空5分，共20分）

13. (2023高二上·深圳期中) 数列 $\text{[math]}$ 的通项公式 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023高二上·深圳期中) 已知直线l： $\text{[math]}$ 被圆C： $\text{[math]}$ （ $\text{[math]}$ ）截得的弦长为2，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2023高二上·深圳期中) 已知椭圆C： $\text{[math]}$ （ $\text{[math]}$ ）的左、右两焦点分别是 $\text{[math]}$ 、 $\text{[math]}$ ，其中 $\text{[math]}$ ．椭圆C上存在一点A ，满足 $\text{[math]}$ ，则椭圆的离心率的取值范围是．

答案解析收藏纠错 + 选题
16. (2023高二上·深圳期中) 已知A ， B分别是椭圆E： $\text{[math]}$ 的左、右顶点，C ， D是椭圆上异于A ， B的两点，若直线AC ， BD的斜率 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，则直线CD过定点，定点坐标为．

答案解析收藏纠错 + 选题

四、解答题（共6小题，17题10分，18-22题12分）

17. (2023高二上·深圳期中) 在平面直角坐标系xOy中，圆 $\text{[math]}$ ： $\text{[math]}$ 与圆 $\text{[math]}$ ： $\text{[math]}$ 相交于P ， Q两点．
1. （1）求线段PQ的长；
2. （2）记圆 $\text{[math]}$ 与x轴正半轴交于点M ，点N在圆 $\text{[math]}$ 上滑动，求 $\text{[math]}$ 面积最大时的直线MN的方程．
答案解析收藏纠错 + 选题
18. (2023高二上·深圳期中) 已知等差数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为等比数列，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求数列 $\text{[math]}$ ， $\text{[math]}$ 的通项公式；
2. （2）求数列 $\text{[math]}$ 的前n项和 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2023高二上·深圳期中) 已知半径为3的圆的圆心在x轴上，圆心的横坐标是整数，且与直线 $\text{[math]}$ 相切．
1. （1）求圆的方程；
2. （2）设直线 $\text{[math]}$ 与圆相交于A ， B两点，求实数a的取值范围；
3. （3）在（2）的条件下，是否存在实数a ，使得弦AB的垂直平分线l过点 $\text{[math]}$ ？若存在，求出实数a的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
20. (2023高二上·深圳期中) 在平面直角坐标系xOy中，圆 $\text{[math]}$ ： $\text{[math]}$ ，圆 $\text{[math]}$ ： $\text{[math]}$ ，点 $\text{[math]}$ ，一动圆M与圆 $\text{[math]}$ 内切、与圆 $\text{[math]}$ 外切．
1. （1）求动圆圆心M的轨迹方程E；
2. （2）是否存在一条过定点的动直线l ，与（1）中的轨迹E交于A、B两点，并且满足HA⊥HB？若存在，请找出定点；若不存在，请说明理由．
答案解析收藏纠错 + 选题
21. (2023高二上·深圳期中) 已知等差数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ，且 $\text{[math]}$ ，数列 $\text{[math]}$ 的前n项之积为 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ ；
2. （2）令 $\text{[math]}$ ，求正整数n ，使得“ $\text{[math]}$ ”与“ $\text{[math]}$ 是 $\text{[math]}$ ， $\text{[math]}$ 的等差中项”同时成立；
3. （3）设 $\text{[math]}$ ， $\text{[math]}$ ，求数列 $\text{[math]}$ 的前2n项和 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2023高二上·深圳期中) 已知椭圆C： $\text{[math]}$ （ $\text{[math]}$ ）的左、右焦点为 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ ， P为椭圆C上异于长轴端点的一个动点，O为坐标原点，直线 $\text{[math]}$ ， PO ， $\text{[math]}$ 分别与椭圆C交于另外三点M ， Q ， N ，当P为椭圆上顶点时，有 $\text{[math]}$ ．
1. （1）求椭圆C的标准方程；
2. （2）求 $\text{[math]}$ 的最大值。
答案解析收藏纠错 + 选题