山西省吕梁市兴县魏家滩中学2023-2024学年八年级上学期...

更新时间：2023-12-25 浏览次数：34 类型：期中考试

一、选择题（本大题共10个小题，每小题3分，共30分.在每个小题给出的四个选项中，只有一项符合题目要求，请把正确答案的代号填在下表中）

1. (2023八上·兴县期中) 100的算术平方根为（）

A . 10 B . $\text{[math]}$ C . $\text{[math]}$ D . 100

答案解析收藏纠错 + 选题
2. (2023八上·兴县期中) 如图，小明从边长为 $\text{[math]}$ 的正方形纸片中剪去边长为 $\text{[math]}$ 的小正方形纸片，则图中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八上·兴县期中) 下列计算中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八上·兴县期中) 下列命题中，属于真命题的是（）

A . 8的立方根是 $\text{[math]}$ B . $\text{[math]}$ 是无理数 C . 0的平方根是0 D . $\text{[math]}$ 的相反数是2

答案解析收藏纠错 + 选题
5. (2023八上·兴县期中) 如图，已知 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八上·兴县期中) 如图，公元1261年，我国南宋数学家杨辉用下图解释二项和的乘方规律，比欧洲的发现要早三百多年，我们把这个三角形称为“杨辉三角”，观察图形可知， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
7. (2023八上·兴县期中) 如图，美美不小心在课后作业的第1题滴了一点墨水，留下一道残缺不全的题目，则被墨水覆盖的部分为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八上·兴县期中) 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一条直线上， $\text{[math]}$ ， $\text{[math]}$ ，要使 $\text{[math]}$ ，还需要添加的条件是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023八上·兴县期中) 一头非洲大象质量的最高纪录为 $\text{[math]}$ ，则 $\text{[math]}$ 头这样的大象的质量为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
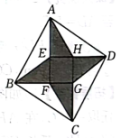
10. (2023八上·兴县期中) 四个全等的直角三角形纸片围成一个大正方形 $\text{[math]}$ ，中间是一个小正方形 $\text{[math]}$ ，连接四条线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 得到如图所示的图形，已知每个直角三角形纸片两条直角边长分别 $\text{[math]}$ ， $\text{[math]}$ （即 $\text{[math]}$ ， $\text{[math]}$ ），图中阴影部分的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共5个小题，每小题3分，共15分）

11. (2024七下·望城月考) $\text{[math]}$ 无理数.（填“是”或“不是”）

答案解析收藏纠错 + 选题
12. (2024九上·长沙开学考) 因式分解 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
13. (2023八上·兴县期中) 若实数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
14. (2023八上·兴县期中) 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中，边 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ，当只添加一个条件时，可使 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2023八上·兴县期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ 是 $\text{[math]}$ 外一点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上的一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题

三、解答题（本大题共8个小题，共75分.解答应写出文字说明，证明过程或演算步骤）

16. (2023八上·兴县期中) 计算题
1. （1）计算： $\text{[math]}$ .
2. （2）化简： $\text{[math]}$ .
答案解析收藏纠错 + 选题
17. (2023八上·兴县期中) 如图，已知点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2023八上·西安月考) 已知 $\text{[math]}$ 的平方根为 $\text{[math]}$ ， $\text{[math]}$ 的立方根为 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的值.
2. （2）求 $\text{[math]}$ 的算术平方根.
答案解析收藏纠错 + 选题
19. (2023八上·兴县期中) 如图，一游戏规则如下：请同学们心里想一个非零的实数，然后各自把这个数按照下面的程序进行计算.
1. （1）当输入的实数 $\text{[math]}$ 为 $\text{[math]}$ 时，求输出的值是多少.
2. （2）小康说：“无论同学们心里想的是哪个实数，我都可以准确地说出计算结果.”你认为小康的说法正确吗？请判断并说明理由.
答案解析收藏纠错 + 选题
20. (2023八上·兴县期中) 如图，一架梯子 $\text{[math]}$ 斜靠在墙 $\text{[math]}$ 上，墙 $\text{[math]}$ 与地面 $\text{[math]}$ 垂直，当梯子的顶端 $\text{[math]}$ 向下滑到点 $\text{[math]}$ 处时，梯子的底端 $\text{[math]}$ 向外滑到点 $\text{[math]}$ 处，经测量得 $\text{[math]}$ .
1. （1）请问 $\text{[math]}$ 吗？请判断并说明理由.
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题

21. (2023八上·兴县期中) 阅读与思考

提出命题	如果一个角的两边与另一角的两边互相垂直，那么这两个角相等
⑴判断真假	这个命题是 ▲ 命题（填“真”或“假”）
⑵求证过程	①若是真命题，请证明； ②若是假命题，请举出一个反例（要求画出相应的图形，并用文字语言或符号语言叙述所举的反例）
⑶结论应用	若两个角的两边互相垂直，且一个角比另一个角的2倍少 $\text{[math]}$ ，则这两个角的度数分别为 ▲ （直接写出结果）

答案解析收藏纠错 + 选题

22. (2023八上·兴县期中) 综合与实践
1. （1）【基础巩固】如图1，已知 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，求证： $\text{[math]}$ .
2. （2）【深入探究】如图2，在（1）的条件下，过点 $\text{[math]}$ ， $\text{[math]}$ 分别作 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ .
  ①试判断 $\text{[math]}$ 与 $\text{[math]}$ 是否全等，并证明你的结论.
  ②当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的长.
3. （3）【拓展探究】如图3，要测量河流 $\text{[math]}$ 的长，因为无法测河流附近的点 $\text{[math]}$ ，可以在 $\text{[math]}$ 外任取一点 $\text{[math]}$ ，在 $\text{[math]}$ 的延长线上任取一点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，并且延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ；延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长到点 $\text{[math]}$ ，使点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一条江线上，若测量出 $\text{[math]}$ 米，则河流 $\text{[math]}$ 米，请说明理由.
答案解析收藏纠错 + 选题
23. (2023八上·兴县期中) 综合与探究
如图，在数轴上，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所表示的数分别为0，1， $\text{[math]}$ ，点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离与点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离相等，设点 $\text{[math]}$ 在数轴上表示的数为 $\text{[math]}$ （点 $\text{[math]}$ 在点 $\text{[math]}$ 的左边）.
1. （1）求 $\text{[math]}$ 的值.
2. （2）在数轴上有两点 $\text{[math]}$ ， $\text{[math]}$ 表示的数为 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的平方根.
3. （3）现将点 $\text{[math]}$ 向左移动5个单位长度得到点 $\text{[math]}$ ，设点 $\text{[math]}$ 表示的数为 $\text{[math]}$ ，在数轴上是否存在一点 $\text{[math]}$ 所表示的数 $\text{[math]}$ ，使得 $\text{[math]}$ .若存在，求出 $\text{[math]}$ 的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题