 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 



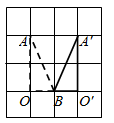 B .
B . 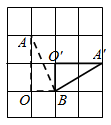 C .
C . 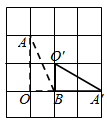 D .
D . 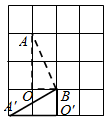

①;
②;
③;
④ .
其中正确的有( )
解:设 , 则原方程变为:
, 解得,
,
.
当时,
, 解得
,
;
当时,
, 解得
,
;
∴原方程的解为: ,
,
,
.
上面解方程的方法简称换元法.
请利用上述方法,解方程:


水平距离x/m | 0 | 1 | 2 | 3 | 4 | |
竖直高度y/m | 2.0 | 3.0 | 3.6 | 3.8 | 3.6 |
①在平面直角坐标系xOy中,描出上表中各对对应值为坐标的点,并用平滑的曲线连接;

②结合表中数据和所画图象,直接写出篮球运行的最高点距离地面的竖直高度是 m,并求y与x满足的函数解析式;
③已知此时韩旭距篮筐中心的水平距离5m,韩旭第一次投篮练习是否成功,请说明理由;