一、选择题：本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项最符合题目要求．
-
A . 直线x＝3
B . 直线x＝－5
C . 直线x＝－1
D . 直线x＝1
-
A . 在一个只装有白球的袋中，摸出黑球
B . a是实数，|a|≥0
C . 在一张纸上任意画两条线段，这两条线段相交
D . 两数相加，和是正数
-
A . y＝(x－4)2
B . y＝(x＋2)2
C . y＝(x－1)2＋3
D . y＝(x－1)2－3
-
-
5.
(2023九上·杭州月考)
函数y＝kx＋k和函数y＝－kx
2＋4x＋4(k是常数，且k≠0)在同一平面直角坐标系中的图象可能是（ ）
-
A . 当x＝1时，y有最大值2
B . 当x＞1时，y随x的增大而减小
C . 当x取0和2时，所得到的y的值相同
D . 图象与y轴的交点坐标是(0，2)
-
A . x＜0或x＞2
B . x＜1或x＞3
C . 0＜x＜2
D . 1＜x＜3
-
8.
(2023九上·萧山月考)
地面上一个小球被推开后笔直滑行，滑行的距离s与时间t的函数关系如图中的部分抛物线所示(其中P是该抛物线的顶点)，下列说法正确的是（ ）
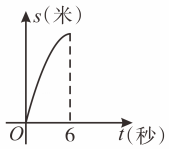
A . 小球滑行6秒停止
B . 小球滑行12秒停止
C . 小球滑行6秒回到起点
D . 小球滑行12秒回到起点
-
A . y＝－4(x－m)2－m2－2
B . y＝－(x＋a)(x－a＋1)
C . y＝－x2－(a＋3)x＋(－
a)
D . y＝ax2－bx＋b－a
-
10.
(2023九上·杭州月考)
已知y关于x的二次函数y＝a(x－m)(x－n)(a≠0)，其图象与y关于x的函数y＝kx＋b的图象交于点(1，y
1)，(6，y
2)，则下面判断正确的是（ ）
A . 若m＋n＞7，a＞0，则k＞0
B . 若m＋n＞7，a＜0，则k＜0
C . 若m＋n＜7，a＞0，则k＜0
D . 若m＋n＜7，a＜0，则k＜0
二、填空题：本题有6个小题，每小题4分，共24分．
-
-
-
13.
(2023九上·萧山月考)
一个布袋里放有5个红球，3个球黄球和2个黑球，它们除颜色外其余都相同，则任意摸出一个球是黑球的概率是
．
-
-
-
16.
(2023九上·杭州月考)
已知y关于x的二次函数y＝(x－m)
2－(x－m)，图象对称轴为直线x＝n，则n，m满足的关系式是
；若把该函数图象向上平移k个单位，使得对于任意的x都有y＞0，则k的取值范围是
．
三、解答题：本题有7小题，共66分．解答应写出文字说明、证明过程或演算步骤．
-
17.
(2023九上·杭州月考)
已知二次函数y＝－(x＋1)
2＋4的图像如图所示，请在同一坐标系中画出二次函数y＝－(x－2)
2＋7的图像．
-
-
-
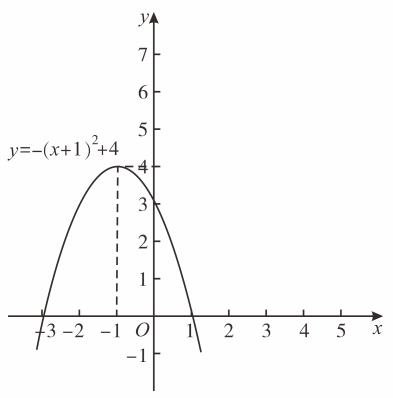
（1）
从布袋里任意摸出一个小球，求上面的数字恰好是“3”的概率.
-
（2）
从布袋里任意摸出一个小球，记录其数字，放回并摇匀，再从中任意摸出一个小球，记录其数字，求两次记录的数字之和为3的概率.（要求列表或画树状图说明）
-
20.
(2023九上·杭州月考)
如图，在矩形ABCD中，AB＝2，BC＝4，E，F，G，H四点依次是边AB，BC，CD，DA上一点（不与各顶点重合），且AE＝AH＝CG＝CF，记四边形EFGH面积为S（图中阴影），AE＝x．
-
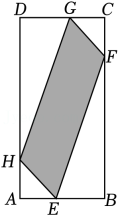
（1）
求S关于x的函数表达式，并直接写出自变量的取值范围．
-
（2）
求x为何值时，S的值最大，并写出S的最大值．
-
-
-
（2）
判断点Q(m ， 4)是否在该函数图象上？若在，求m的值，若不在，说明理由．
-
22.
(2023九上·萧山月考)
如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（ 
， 
）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．
-
-
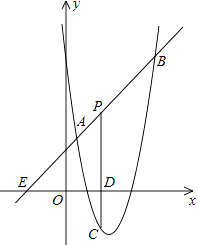
（2）
是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由．
-
23.
(2023九上·萧山月考)
某款旅游纪念品很受游客喜爱，每个纪念品进价40元，规定销售单价不低于44元，且不高于52元．某商户在销售期间发现，当销售单价定为44元时，每天可售出300个，销售单价每上涨1元，每天销量减少10个．现商家决定提价销售，设每天销售量为y个，销售单价为x元．
-
（1）
直接写出y与x之间的函数关系式和自变量x的取值范围；
-
（2）
将纪念品的销售单价定为多少元时，商家每天销售纪念品获得的利润w元最大？最大利润是多少元？
-
（3）
该商户从每天的利润中捐出200元做慈善，为了保证捐款后每天剩余利润不低于2200元，求销售单价x的范围．
-
-
（1）
若该图象过点(1，－3)，求这个二次函数的表达式．
-
（2）
(x
1 ， y
1)，(x
2 ， y
2)是该函数图象上的两个不同点，
①若x1＋x2＝4时，有y1＝y2 ， 求a的值；
②当x1＞x2≥－3时，恒有y1＞y2 ， 试求a的取值范围．
B . 
C . 
D . 
