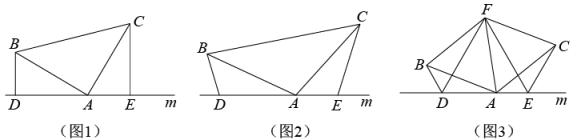
B .
B .  C .
C .  D .
D . 
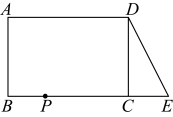
① ;②PQ∥AE; ③
;④
;⑤
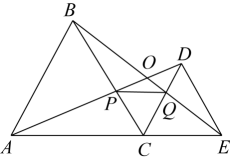
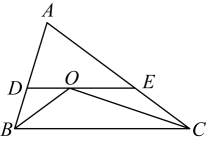
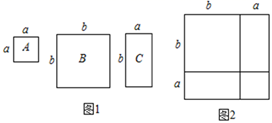
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
要把多项式分解因式,可以先把它的前两项分成一组,并提出a , 再把它的后两项分成一组,并提出b , 从而得
.
这时,由于中又有公因式
, 于是可提公因式
, 从而得到
, 因此有
.
这种因式分解的方法叫做“分组分解法”,如果把一个多项式各个项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以利用分组分解法来分解因式.
①;
②;
③ .