广东省深圳市南山区南山中英文学校2023-2024学年第一学...

更新时间：2024-04-19 浏览次数：16 类型：月考试卷

一、选择题（每题3分，共30分）

1. 方程x²＝3x的解是（　　）

A . x＝3 B . x＝0 C . x₁＝3，x₂＝0 D . x₁＝﹣3，x₂＝0

答案解析收藏纠错 + 选题
2. 下列各选项中，其主视图如图所示的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. 2020年9月1日，《深圳市生活垃圾分类管理条例》正式实施．滨海学校九（1）班成立了“环保卫士”宣传小组，其中男生2人，女生3人，从中随机抽取一名同学进社区宣传“垃圾分类”，恰好抽到女生的概率为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 已知（﹣1，4）是反比例函数y＝ $\text{[math]}$ 上一点，下列各点不在y＝ $\text{[math]}$ 上的是（　　）

A . （﹣3， $\text{[math]}$ ） B . （2，2） C . （4，﹣1） D . （﹣ $\text{[math]}$ ， 8）

答案解析收藏纠错 + 选题
5. 把二次函数y＝﹣x²﹣2x+3配方化为y＝a（x﹣h）²+k形式是（　　）

A . y＝﹣（x﹣1）²﹣4 B . y＝﹣（x+1）²+4 C . y＝﹣（x﹣1）²+3 D . y＝﹣（x+1）²﹣3

答案解析收藏纠错 + 选题
6. 如图，在△ABC中，BD⊥AC于点D，AE⊥BC于点E，交BD于点F，下列三角形中不一定与△BCD相似的是（　　）

A . △BFE B . △AFD C . △ACE D . △BAE

答案解析收藏纠错 + 选题
7. 下列命题是真命题的是（　　）

A . 三角形的内心到三角形三个顶点的距离相等 B . 若关于x的方程kx²+2x﹣1＝0有实数根，则k的取值范围是k≥﹣1且k≠0 C . 若关于x的一元一次不等式组 $\text{[math]}$ 无解，则a的范围是a≤3 D . 若点C是线段AB的黄金分割点，则 $\text{[math]}$

答案解析收藏纠错 + 选题
8. 如图，一次函数y＝ax+b与反比例函数 $\text{[math]}$ 的图象交于点A（1，m），B（﹣2，n），则关于x的不等式ax+b＞ $\text{[math]}$ 的解集是（　　）

A . x＞2或﹣1＜x＜0 B . x＞1或﹣2＜x＜0 C . x＜﹣1或0＜x＜2 D . 0＜x＜1或x＜﹣2

答案解析收藏纠错 + 选题
9. 抛物线y＝ax²+bx+c的大致图象如图所示，则下列说法中错误的是（　　）

A . abc＜0 B . 3a+c＜0 C . 当x＝t时，y＞0，若x＝t﹣4，则y＜0 D . a（x²﹣1）+b（x﹣1）＞0

答案解析收藏纠错 + 选题
10. 如图，在正方形ABCD中，AD＝4，E为CD中点，F为BC上的一点，且∠EAF＝45°，∠ABG＝∠DAE，连接EF，延长BG交AE于点M，交AD于点N，则以下结论；
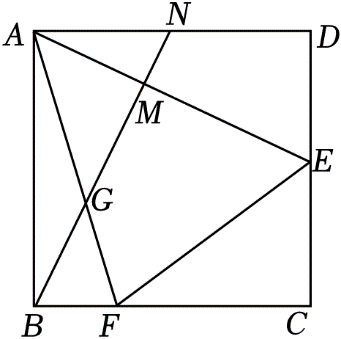
①DE+BF＝EF②BN⊥AE③BF＝ $\text{[math]}$ ④S_△_BGF＝ $\text{[math]}$ 中正确的是（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（每题3分，共15分）

11. 已知x＝﹣2是方程x²﹣kx+1＝0的根，则k的值为．

答案解析收藏纠错 + 选题
12. 在某一时刻，一根长为1.5m的竹竿投影在地面上的影长是1m，此刻测得旗杆投影在地面上的影长是12m，则旗杆的高度为m．

答案解析收藏纠错 + 选题
13. 如图，将一副三角板△ABC和△BCD拼在一起，E为AC的中点，将△ABE沿BE翻折得到△A'BE，连接DE，若BC＝2 $\text{[math]}$ ，则DE＝．

答案解析收藏纠错 + 选题
14. 如图，某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动，此时无人机在高地面30米的点D处，操控者站在点A处，无人机测得点A的俯角为30°．测得教学楼楼顶点C处的俯角为45°，操控者和教学楼BC的距离为60米，则教学楼BC的高度是米．

答案解析收藏纠错 + 选题
15. 如图，已知梯形ABCO的底边AO在x轴上，BC∥AO，AB⊥AO，过点C的双曲线 $\text{[math]}$ 交OB于D，且OD：DB＝1：2，若△OBC的面积等于3，则k的值是．

答案解析收藏纠错 + 选题

三、解答题（共55分）

16. 计算：
1. （1） 2sin²45°﹣6cos30°+3tan45°+4sin60°；
2. （2）解方程：3x（x﹣1）＝2﹣2x．
答案解析收藏纠错 + 选题
17. 随着时代发展，人们乘坐公交车支付车票的方式更加多样、便捷，某校数学实践小组设计了一份公交车票支付方式调查问卷，要求每位被调查人选且只选一种最喜欢的支付方式．现将调查结果进行统计并绘制成如下两幅不完整的统计图．
根据所给的信息解答下列问题：
1. （1）这次活动共调查了人；在扇形统计图中，表示“微信”支付的扇形圆心角的度数为；
2. （2）将条形统计图补充完整；
3. （3）小明和小亮都没有公交卡，在乘车中，想从“微信”“支付宝”“现金”“云闪付”四种支付方式中选一种方式进行支付，请用画树状图或列表格的方法，求出两人恰好选择同一种支付方式的概率．
答案解析收藏纠错 + 选题
18. 清明是二十四节气之一，也是我国的传统节日，清明节吃青团是很多地方的习俗．清明节前市场上肉松蛋黄青团比芝麻青团的进价每盒便宜10元，某商家用800元购进的芝麻青团和用600元购进的肉松蛋黄青团盒数相同．在销售中，该商家发现芝麻青团每盒售价50元时，每天可售出100盒，当每盒售价提高1元时，每天少售出2盒．
1. （1）求芝麻青团和肉松蛋黄青团的进价；
2. （2）已知芝麻青团每盒的售价不高于65元，W表示该商家每天销售芝麻青团的利润（单位；元），芝麻青团每盒售价为多少元时，一天获得利润最大？最大利润是多少元？
答案解析收藏纠错 + 选题
19. (2020九上·罗湖期末) 如图，某数学兴趣小组为测量一棵古树BH和教学楼CG的高，先在A处用高2米的测角仪测得古树顶端H的仰角∠HDE为45°，此时教学楼顶端G恰好在视线DH上，再向前走6米到达B处，又测得教学楼顶端G的仰角∠GEF为60°，点A、B、C三点在同一水平线上．
1. （1）计算古树BH的高；
2. （2）计算教学楼CG的高．（结果保留根号）
答案解析收藏纠错 + 选题
20. 如图，在直角坐标系中有一Rt△AOB，O为坐标原点，OA＝1，tan∠BAO＝3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y＝ax²+bx+c经过点A，B，C．
1. （1）求抛物线的解析式；
2. （2）若点P是第二象限内抛物线上的动点，其横坐标为t，是否存在一点P，使△PCD的面积最大？若存在，求出△PCD面积的最大值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
21. 请阅读下列解题过程；解一元二次不等式；x²﹣2x﹣3＜0．
解；设x²﹣2x﹣3＝0，解得；x₁＝﹣1，x₂＝3．
则抛物线y＝x²﹣2x﹣3与x轴的交点坐标为（﹣1，0）和（3，0）．
画出二次函数y＝x²﹣2x﹣3的大致图象（如图1所示）．
由图象可知；当﹣1＜x＜3时函数图象位于x轴下方，
此时y＜0，即x²﹣2x﹣3＜0．
所以一元二次不等式x²﹣2x﹣3＜0的解集为：﹣1＜x＜3．
通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：
1. （1）用类似的方法解一元二次不等式；﹣x²+4x﹣3＞0．
2. （2）某“数学兴趣小组”根据以上的经验，对函数y＝﹣（x﹣1）（|x|﹣3）的图象和性质进行了探究，探究过程如下；
  ①列表；x与y的几组对应值如表，其中m＝ ▲ ．
  x
  …
  ﹣4
  ﹣3
  ﹣2
  ﹣1
  0
  1
  2
  3
  4
  …
  y
  …
  5
  0
  ﹣3
  m
  ﹣3
  0
  1
  0
  ﹣3
  …
  ②如图2，在直角坐标系中画出了函数y＝﹣（x﹣1）（|x|﹣3）的部分图象，用描点法将这个图象补画完整．
  ③结合函数图象，解决下列问题；不等式﹣4≤﹣（x﹣1）（|x|﹣3）≤0的解集为： ▲ ．
答案解析收藏纠错 + 选题
22. 如图1，正方形ABCD中，AC为对角线，点P在线段AC上运动，以DP为边向右作正方形DPFE，连接CE；
1. （1）【初步探究】
  则AP与CE的数量关系是，AP与CE的夹角度数为；
2. （2）【探索发现】
  点P在线段AC及其延长线上运动时，如图1，图2，探究线段DC，PC和CE三者之间的数量关系，并说明理由；
3. （3）【拓展延伸】
  点P在对角线AC的延长线上时，如图3，连接AE，若AB＝2 $\text{[math]}$ ， AE＝ $\text{[math]}$ ，求四边形DCPE的面积．
答案解析收藏纠错 + 选题