 B .
B .  C .
C .  D .
D . 




①请说明:;
②求出周长的最小值;

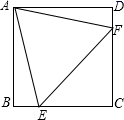
由两个顶角相等且有公共顶角顶点的特殊多边形组成的图形,如果把它们的底角顶点连接起来,则在相对位置变化的过程中,始终存在一对全等三角形,我们把这种模型称为“手拉手模型”.在如图①所示的“手拉手”图形中,小白发现若 ,
,
, 则
, 请证明他的发现;
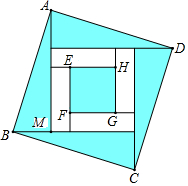
如图②, , 试探索线段
之间满足的等量关系,并证明;
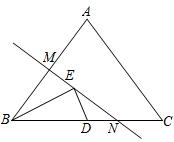
如图③,和
是拥有公共顶点C的两个等边三角形,M点、N点、F点分别是
的中点.当
时,请直接写出
的长.
已知,等腰三角形纸片ABC中,AB=AC,∠BAC=36°.现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).下面是小文借助尺规解决这一问题的过程,请阅读后完成相应任务.

作法:如图1所示, ①分别作AB,AC的垂直平分线,交于点P; ②连接PA,PB,PC. 结论:沿线段PA,PB,PC剪开,即可得到三个等腰三角形, 理由:∵点P在线段AB的垂直平分线上, ∴…….. (依据). 同理,PA=PC. ∴PA=PB=PC. ∴△PAB、△PBC、△PAC都是等腰三角形 |
任务:
A.请在图3中设计出一种裁剪方案,将该三角形纸片分成三个等腰三角形(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).
B.请在图3中设计出一种裁剪方案,将该三角形纸片分成四个等腰三角形,且四个三角形互不全等(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).
勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法.如图.

把两个全等的直角三角形如图1放置,其三边长分别为 ,
,
. 显然,
,
. 请用
,
,
分别表示出梯形
, 四边形
,
的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
,
,
,则它们满足的关系式为,经化简,可得到勾股定理.
借助上面的思考过程,画图说明并求代数式的最小值
.