一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
-
-
-
-
6.
(2024高三上·长沙期末)
已知抛物线
E:

(

)点为
F , 准线为
l , 过
E上的一点
A作
l的垂线,垂足为
B , 若

(
O为坐标原点),且△
ABF的面积为

, 则
E的方程为( )
-
7.
(2024高三上·安顺期末)
一个轴截面是边长为

的正三角形的圆锥型封闭容器内放入一个半径为1的小球

后,再放入一个球

, 则球

的表面积与容器表面积之比的最大值为( )
-
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0.
-
A . 若 且
且 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 , 则
, 则
-
10.
(2024高三上·长沙期末)
某食品的保鲜时间
y(单位:小时)与储藏温度
x(单位:℃)满足函数关系

(

…为自然对数的底数,
k ,
b为常数).若该食品在0℃的保鲜时间是192小时,在14℃的保鲜时间是48小时(参考数据:

,

),则下列说法正确的是( )
A .  B . 若该食品储藏温度是21℃,则它的保鲜时间是16小时
C .
B . 若该食品储藏温度是21℃,则它的保鲜时间是16小时
C .  D . 若该食品保鲜时间超过96小时,则它的储藏温度不高于7℃
D . 若该食品保鲜时间超过96小时,则它的储藏温度不高于7℃
-
11.
(2024高三上·贵州模拟)
欧拉函数

(

)的函数值等于所有不超过正整数
n , 且与
n互质的正整数的个数(公约数只有1的两个正整数称为互质整数),例如:

,

, 则( )
A .  B . 当n为奇数时,
B . 当n为奇数时, C . 数列
C . 数列 为等比数列
D . 数列
为等比数列
D . 数列 的前n项和小于
的前n项和小于
-
12.
(2024高三上·贵州模拟)
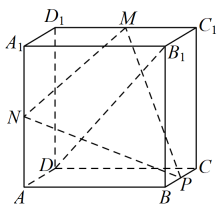
如图,在棱长为2的正方体

中,已知
M ,
N ,
P分别是棱

,

,

的中点,
Q为平面

上的动点,且直线

与直线

的夹角为

, 则( )
A .  平面
平面 B . 平面
B . 平面 截正方体所得的截面面积为
截正方体所得的截面面积为 C . 点Q的轨迹长度为
C . 点Q的轨迹长度为 D . 能放入由平面PMN分割该正方体所成的两个空间几何体内部(厚度忽略不计)的球的半径的最大值为
D . 能放入由平面PMN分割该正方体所成的两个空间几何体内部(厚度忽略不计)的球的半径的最大值为
三、填空题:本题共4小题,每小题5分,共20分.
-
-
14.
(2024高三上·长沙期末)
某市统计高中生身体素质的状况,规定身体素质指标值不小于60就认为身体素质合格.现从全市随机抽取100名高中生的身体素质指标值

(

, 2,3,…,100),经计算

,

. 若该市高中生的身体素质指标值服从正态分布

, 则估计该市高中生身体素质的合格率为
.(用百分数作答,精确到0.1%)
参考数据:若随机变量X服从正态分布 , 则
, 则 ,
,
 ,
,  .
.
-
-
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
-
(1)
求

;
-
-
18.
(2024高三上·长沙期末)
已知△
ABC的内角
A ,
B ,
C的对边分别为
a ,
b ,
c ,
A为锐角,△
ABC的面积为
S ,

.
-
-
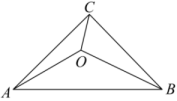
(2)
如图,若

,

,
O为△
ABC内一点,且

,

, 求
OB的长.
-
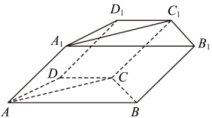
19.
(2024高三上·长沙期末)
如图,已知斜四棱柱

, 底面
ABCD为等腰梯形,
AB∥
CD , 点

在底面
ABCD的射影为
O , 且

,

,

,

.
-
(1)
求证:平面
ABCD⊥平面

;
-
(2)
若
M为线段

上一点,且平面
MBC与平面
ABCD夹角的余弦值为

, 求直线

与平面
MBC所成角的正弦值.
-
20.
(2024高三上·长沙期末)
杭州亚运会的三个吉祥物是琮琮、宸宸和莲莲,他们分别代表了世界遗产良渚古城遗址、京杭大运河和西湖,分别展现了不屈不挠、坚强刚毅的拼搏精神,海纳百川的时代精神和精致和谐的人文精神. 甲同学可采用如下两种方式购买吉祥物,方式一:以盲盒方式购买,每个盲盒19元,盲盒外观完全相同,内部随机放有琮琮、宸宸和莲莲三款中的一个,只有打开才会知道买到吉祥物的款式,买到每款吉祥物是等可能的;方式二:直接购买吉祥物,每个30元.
-
(1)
甲若以方式一购买吉祥物,每次购买一个盲盒并打开. 当甲买到的吉祥物首次出现相同款式时,用X表示甲购买的次数,求X的分布列;
-
(2)
为了集齐三款吉祥物,甲计划先一次性购买盲盒,且数量不超过3个,若未集齐再直接购买吉祥物,以所需费用的期望值为决策依据,甲应一次性购买多少个盲盒?
-
-
-
(2)
设点

,

,

, 直线
AM ,
AN分别与曲线
E交于点
S ,
T(
S ,
T异于
A),

, 垂足为
H , 求

的最小值.
-
-
(1)
讨论函数

的单调性;
-
(2)
已知

, 若

,

, 当

时,

恒成立,求
k的最大值.
 B .
B . 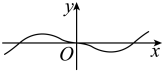 C .
C . 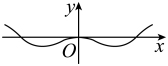 D .
D . 
, 则
,
,
.
