广东省河源市紫金县2023-2024学年八年级上学期期末数学...

更新时间：2024-05-15 浏览次数：23 类型：期末考试

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2024八上·毕节期中) 在下列各组数中，是勾股数的是（）

A . 1，2，3 B . 0.3，0.4，0.5 C . 6，8，10 D . 4，5，6

答案解析收藏纠错 + 选题
2. (2024八上·紫金期末) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八上·紫金期末) 若点 $\text{[math]}$ 在 $\text{[math]}$ 轴的下方、 $\text{[math]}$ 轴的左方，到每条坐标轴的距离都是5，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八上·紫金期末) 在平面直角坐标系中，点 $\text{[math]}$ 与点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称，则点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八上·紫金期末) 如图，下列条件中，不能判断直线 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八上·南海月考) 下列关于一次函数 $\text{[math]}$ 的说法中，正确的是（）

A . 图象必经过点 $\text{[math]}$ B . 图象经过一、二、三象限 C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大

答案解析收藏纠错 + 选题
7. (2024八上·紫金期末) 已知 $\text{[math]}$ 和 $\text{[math]}$ 是二元一次方程 $\text{[math]}$ 的两个解，则 $\text{[math]}$ ， $\text{[math]}$ 的值分别为（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， C . $\text{[math]}$ ， $\text{[math]}$ D . ， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·兴宁模拟) 某校篮球队有14名队员，队员的年龄情况统计如下表：
年龄/岁
15
16
17
18
人数
3
4
5
2
则这14名队员年龄的中位数和众数分别是（）

A . 17，16 B . 16.5，17 C . 16，17 D . 16.5，16

答案解析收藏纠错 + 选题
9. (2024八上·龙岗期中) 某公司市场营销部的个人月收入与其每月的销售量成一次函数关系，其图象如图所示，由图中给出的信息可知，营销人员没有销售时的收入是（）

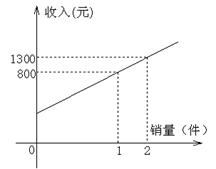
A . 310元 B . 300元 C . 290元 D . 280元

答案解析收藏纠错 + 选题
10. (2024八上·紫金期末) 两条直线 $\text{[math]}$ 与 $\text{[math]}$ 在同一平面直角坐标系中的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题：本大题共6小题，每小题3分，共18分.

11. (2024八上·紫金期末) 比较实数的大小：4 $\text{[math]}$ （填“>”“<”或“=”）.

答案解析收藏纠错 + 选题
12. (2024八上·紫金期末) 有一组数据：1，3，5，则这组数据的方差是.

答案解析收藏纠错 + 选题
13. (2024七下·临沭月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的立方根是.

答案解析收藏纠错 + 选题
14. (2024八上·紫金期末) 如图，将直尺与含30°角的三角尺摆放在一起，若∠1=20°，则∠2的度数是.

答案解析收藏纠错 + 选题
15. (2024八上·紫金期末) 我国古代数学著作《九章算术》中有这样一个问题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”意思是：“几个人一起去购买某物品，每人出8钱，则多出3钱；每人出7钱，则还差4钱.问人数、物品的价格分别是多少？”设该问题中的人数为 $\text{[math]}$ 人，物品的价格为 $\text{[math]}$ 钱，则可列二元一次方程组为.

答案解析收藏纠错 + 选题
16. (2024八上·紫金期末) 如图，在平面直角坐标系中，直线为正比例函数 $\text{[math]}$ 的图象，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线交直线于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边作第一个正方形 $\text{[math]}$ ；过点 $\text{[math]}$ 作直线的垂线，垂足为点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边作第二个正方形 $\text{[math]}$ ；过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，垂足为点 $\text{[math]}$ ，交直线于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边作第三个正方形 $\text{[math]}$ ， …，依此类推，则第2024个正方形 $\text{[math]}$ 的面积是.

答案解析收藏纠错 + 选题

三、解答题：本大题共9小题，共72分.解答应写出文字说明、证明过程或演算步骤.

17. (2024八上·紫金期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2024八上·紫金期末) 解二元一次方程组： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2024八上·紫金期末) 如图，在平面直角坐标系中， $\text{[math]}$ 的顶点坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）请画出 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的 $\text{[math]}$ ，并写出点 $\text{[math]}$ 的坐标；
2. （2）在 $\text{[math]}$ 轴上有一点 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是.
答案解析收藏纠错 + 选题
20. (2024八上·紫金期末) 某校八年级260名学生开展“好书伴成长”读书活动，要求每人每学期至少阅读4~7本课外读物，学期结束后随机抽查了若干名学生每人阅读课外书的数量，并分为四种类型， $\text{[math]}$ ：4本； $\text{[math]}$ ：5本； $\text{[math]}$ ：6本； $\text{[math]}$ ：7本，将各类的人数绘制成如图所示的扇形统计图和条形统计图.
图1 图2
1. （1）求这次被调查学生的人数；
2. （2）写出被调查学生每人阅读课外书数量的众数、中位数；
3. （3）求被调查学生每人阅读课外书数量的平均数，并估计这260名学生阅读课外书的总数.
答案解析收藏纠错 + 选题
21. (2024八上·紫金期末) 电力公司为鼓励市民节约用电，采取按月用电量分段收费办法.若某户居民每月应交电费 $\text{[math]}$ （元）与用电量 $\text{[math]}$ （度）的函数图象是一条折线（如图所示），根据图象解下列问题：
1. （1）分别求出当 $\text{[math]}$ 和 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式.
2. （2）若该用户某月用了72度电，则应缴费多少元？
3. （3）若该用户某月缴费105元时，则该用户该月用了多少度电？
答案解析收藏纠错 + 选题
22. (2024八上·紫金期末)
图1 图2
1. （1）如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
2. （2）如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
23. (2024八上·紫金期末) 如图， $\text{[math]}$ 为 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）判断线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的数量关系，并说明理由；
2. （2）连接 $\text{[math]}$ ， $\text{[math]}$ ，若设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，利用此图证明勾股定理.
答案解析收藏纠错 + 选题
24. (2024八上·紫金期末) 已知在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为边 $\text{[math]}$ 延长线上一点， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 为射线 $\text{[math]}$ 上一点.
1. （1）如图，连接 $\text{[math]}$ ， ①若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
  ②若 $\text{[math]}$ 平分 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
2. （2）若直线 $\text{[math]}$ 垂直于 $\text{[math]}$ 的一边，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题
25. (2024八上·紫金期末) 如图，在平面直角坐标系内，点 $\text{[math]}$ 为坐标原点，经过点 $\text{[math]}$ 的直线交 $\text{[math]}$ 轴正半轴于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 交 $\text{[math]}$ 轴负半轴于点 $\text{[math]}$ .
备用图
1. （1）直线 $\text{[math]}$ 的解析式为；直线 $\text{[math]}$ 的解析式为.
2. （2）横坐标为 $\text{[math]}$ 的点 $\text{[math]}$ 在线段 $\text{[math]}$ 上（不与点 $\text{[math]}$ ， $\text{[math]}$ 重合），过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线交 $\text{[math]}$ 于点 $\text{[math]}$ ，设 $\text{[math]}$ 的长为 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式并直接写出相应的 $\text{[math]}$ 的取值范围.
3. （3）在（2）的条件下，在 $\text{[math]}$ 轴上是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 为等腰直角三角形？若存在，求出点 $\text{[math]}$ 的坐标，若不存在，请说明理由.
答案解析收藏纠错 + 选题