重庆市渝北区六校联盟2023-2024学年八年级上学期第二次...

更新时间：2024-04-11 浏览次数：32 类型：期中考试

一、选择题（本大题共10小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

1. (2023八上·渝北期中) 我市积极普及科学防控知识，下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（）

A . 防控疫情我们在一起 B . 有症状早就医 C . 打喷嚏捂口鼻 D . 勤洗手勤通风

答案解析收藏纠错 + 选题
2. (2023八上·渝北期中) 下列运算中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八上·渝北期中) 如图，点A，D，C，F在一条直线上，AB=DE，∠A=∠EDF，补充下列条件不能证明三角形△ABC≌△DEF的是（）

A . AD=CF B . BC∥EF C . ∠B=∠E D . BC=EF

答案解析收藏纠错 + 选题
4. (2023八上·渝北期中) 如果等腰三角形两边长是 $\text{[math]}$ 和 $\text{[math]}$ ，那么它的周长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 16或 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八上·渝北期中) 如图，△ABC是等腰三角形，点O是底边BC上任意一点，OE、OF分别与两边垂直，等腰三角形ABC的腰长为5，面积为12，则OE+OF的值为（）

A . 1.2 B . 2.4 C . 3.6 D . 4.8

答案解析收藏纠错 + 选题
6. (2023八上·渝北期中) 如图，在Rt△ABC中，∠ACB=90°，根据尺规作图的痕迹判断，以下结论中错误的是（）

A . ∠BDE=∠BAC B . ∠BAD=∠B C . DE=DC D . AE=AC

答案解析收藏纠错 + 选题
7. (2023八上·渝北期中) 某商店将某种碳酸饮料每瓶的价格下调了10%．将某种果汁饮料每瓶的价格上调了5%，已知调价前买这两种饮料各一瓶共花费8元，调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费19.8元，若设上述碳酸饮料、果汁饮料在调价前每瓶分别为x元和y元，则可列方程组为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八上·渝北期中) 将大小形状完全相同的“ $\text{[math]}$ ”按如图所示的规律依次摆放，观察每个图中“ $\text{[math]}$ ”的个数，则第 $\text{[math]}$ 个图中三角形的个数是（）

A . 40 B . 42 C . 43 D . 44

答案解析收藏纠错 + 选题
9. (2023八上·渝北期中) 如果关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 有且只有 $\text{[math]}$ 个整数解，且关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的解为非负整数，则符合条件的所有整数 $\text{[math]}$ 的和为（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
10. (2023八上·渝北期中) 有 $\text{[math]}$ 个依次排列的整式：第一项是 $\text{[math]}$ ，第二项是 $\text{[math]}$ ，用第二项减去第一项，所得之差记为 $\text{[math]}$ ，将 $\text{[math]}$ 加 $\text{[math]}$ 记为 $\text{[math]}$ ，将第二项与 $\text{[math]}$ 相加作为第三项，将 $\text{[math]}$ 加 $\text{[math]}$ 记为 $\text{[math]}$ ，将第三项与 $\text{[math]}$ 相加作为第四项，以此类推；某数学兴趣小组对此展开研究，得到 $\text{[math]}$ 个结论：
$\text{[math]}$ ；
$\text{[math]}$ 当 $\text{[math]}$ 时，第 $\text{[math]}$ 项为 $\text{[math]}$ ；
$\text{[math]}$ 若第 $\text{[math]}$ 项与第 $\text{[math]}$ 项之和为 $\text{[math]}$ ，则 $\text{[math]}$ ；
$\text{[math]}$ 第 $\text{[math]}$ 项为 $\text{[math]}$ ；
$\text{[math]}$ 当 $\text{[math]}$ 时， $\text{[math]}$ ；
以上结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共8小题，共32分）将每小题的答案直接填写在答题卡中对应的横线上．）

11. (2023八上·渝北期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023八上·渝北期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2023八上·渝北期中) 一个多边形的内角和是外角和的 $\text{[math]}$ 倍，这个多边形边数是．

答案解析收藏纠错 + 选题
14. (2023八上·渝北期中) 已知点 $\text{[math]}$ 与点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2023八上·渝北期中) 如图，在△ABC中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点．将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在 $\text{[math]}$ 边上的点 $\text{[math]}$ 处，且满足 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2023八上·渝北期中) 如图，△ABC的面积为16，AD平分∠BAC，且AD⊥BD于D，则△ADC的面积为。

答案解析收藏纠错 + 选题
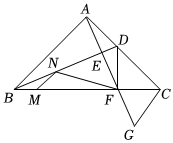
17. (2023八上·渝北期中) 如图， $\text{[math]}$ 是等腰 $\text{[math]}$ 的角平分线， $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线，两线交于点 $\text{[math]}$ 与 $\text{[math]}$ 交于 $\text{[math]}$ ，与 $\text{[math]}$ 交于 $\text{[math]}$ ，连接 $\text{[math]}$ ，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的动点，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的动点，连接 $\text{[math]}$ ， $\text{[math]}$ ，下列四个结论： $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ 其中正确的是 $\text{[math]}$ 填写序号 $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2023八上·渝北期中) 若一个四位数 $\text{[math]}$ 的千位数字与十位数字的和为 $\text{[math]}$ ，百位数字与个位数字的和也为 $\text{[math]}$ ，则这个四位数 $\text{[math]}$ 为“双十数” $\text{[math]}$ 例如： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是“双十数”；又如： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 不是“双十数” $\text{[math]}$ 若一个“双十数” $\text{[math]}$ 的千位数字为 $\text{[math]}$ ，百位数字为 $\text{[math]}$ ，十位数字为 $\text{[math]}$ ，个位数字为 $\text{[math]}$ ，记 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 是整数时， $\text{[math]}$ 的最大值为，若 $\text{[math]}$ 、 $\text{[math]}$ 均为整数时，记 $\text{[math]}$ ，当 $\text{[math]}$ 取得最大值，且 $\text{[math]}$ 时， $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、（解答题：（本大题共7小题，每题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

19. (2023八上·渝北期中) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2023八上·渝北期中) 尺规作图并完成证明：
1. （1）如图，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．尺规作图：作 $\text{[math]}$ 的平分线 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ；
2. （2）证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2023八上·渝北期中) 如图 $\text{[math]}$ 的顶点均在边长为 $\text{[math]}$ 的小正方形网格中的格点上，如图，建立平面直角坐标系，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上．
1. （1）在图中画出 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的 $\text{[math]}$ ，连接 $\text{[math]}$ ，求证： $\text{[math]}$ ≌ $\text{[math]}$ ，
2. （2）请在 $\text{[math]}$ 轴上画点 $\text{[math]}$ ，使得 $\text{[math]}$ 最短． $\text{[math]}$ 保留作图痕迹，不写画法 $\text{[math]}$
答案解析收藏纠错 + 选题
22. (2023八上·渝北期中) 某校为了解八年级学生的视力情况，对八年级的学生进行了一次视力调查，并将调查数据进行统计整理，绘制出如下频数分布表和频数分布直方图的一部分．
视力
频数 $\text{[math]}$ 人 $\text{[math]}$
频率

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$
1. （1）在频数分布表中， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）将频数分布直方图补充完整；
3. （3）若视力在 $\text{[math]}$ 以上 $\text{[math]}$ 含 $\text{[math]}$ 均属正常，求视力正常的人数占被调查人数的百分比是多少？
答案解析收藏纠错 + 选题
23. (2023八上·渝北期中) 如图， $\text{[math]}$ 是等边三角形， $\text{[math]}$ 是 $\text{[math]}$ 边上的高，延长 $\text{[math]}$ 至 $\text{[math]}$ ，使 $\text{[math]}$ ．
1. （1）试说明： $\text{[math]}$ ．
2. （2）过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的周长．
答案解析收藏纠错 + 选题
24. (2023八上·渝北期中) 香椿是大家非常喜欢的时令蔬菜， $\text{[math]}$ 月份是香椿上市的旺季．某蔬菜超市销售香椿，第一周每千克香椿的销售单价比第二周销售单价高 $\text{[math]}$ 元，该蔬菜超市这两周共销售香椿 $\text{[math]}$ 千克，且第一周香椿的销量与第二周的销量之比为 $\text{[math]}$ ： $\text{[math]}$ ，该蔬菜超市这两周香椿销售总额为 $\text{[math]}$ 元．
1. （1）第二周香椿销售单价是每千克多少元？
2. （2）随着香椿的大量上市， $\text{[math]}$ 月份第三周，香椿定价与第二周保持一致，且该蔬菜超市推出会员优惠活动，所有的会员均可享受 $\text{[math]}$ 的价格优惠，而非会员需要按照原价购买，第三周香椿的销量比第二周增加了 $\text{[math]}$ ，其中通过会员优惠活动购买的销量占第三周香椿总销量的 $\text{[math]}$ ，而第三周香椿的销售总额比第二周销售额提高了 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
25. (2023八上·渝北期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的两条高．
1. （1）求证： $\text{[math]}$ ；
2. （2）若过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题

四、解答题：（本大题1个小题，共8分）解答时必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

26. (2023八上·渝北期中)
1. （1）【初步探索】如图 $\text{[math]}$ ：在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，探究图中 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系．
  小王同学探究此问题的方法是：延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ 连接 $\text{[math]}$ ，先证明 $\text{[math]}$ ，再证明 $\text{[math]}$ ，可得出结论，他的结论应是；
2. （2）【灵活运用】如图 $\text{[math]}$ ，若在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，上述结论是否仍然成立，并说明理由；
3. （3）【拓展延伸】如图 $\text{[math]}$ ，已知在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，若点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，如图 $\text{[math]}$ 所示，仍然满足 $\text{[math]}$ ，请写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并给出证明过程．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

重庆市渝北区六校联盟2023-2024学年八年级上学期第二次...

副标题：

*注意事项：

重庆市渝北区六校联盟2023-2024学年八年级上学期第二次...

试题分析

总体分析

题量分析

难度分析

知识点分析

视力	频数 $\text{[math]}$ 人 $\text{[math]}$	频率
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$