贵州省遵义市2023-2024学年八年级上学期1月期末数学试...

更新时间：2024-03-24 浏览次数：30 类型：期末考试

一、单选题（本题共12小题，每小题3分，共36分．在每小题列出的选项中,选出符合题目的一项，用2B铅笔把答题卡上对应题目的答案标号涂黑、涂满．)

1. (2024·官渡模拟) 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产作品录．下面四幅作品分别代表“惊蛰”、“谷雨”、“立秋”、“冬至”，其中是轴对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024八上·遵义期末) 现有两根长度分别为4cm和7cm的木棒．若要钉成一个三角形木架，则应选取的第三根木棒长可以为（　　）

A . 3cm B . 6cm C . 11cm D . 13cm

答案解析收藏纠错 + 选题
3. (2024八上·遵义期末) 人体中枢神经系统中约含有1千亿个神经元，某种神经元的直径约为0.000049．将数据0.000049用科学记数法表示为（　　）

A . 4.9×10^﹣5 B . 4.9×10^﹣6 C . 0.49×10^﹣6 D . 49×10^﹣6

答案解析收藏纠错 + 选题
4. (2024八下·商水月考) 化简： $\text{[math]}$ 的结果是（　　）

A . $\text{[math]}$ B . 1 C . 2 D . 0

答案解析收藏纠错 + 选题
5. (2024八上·遵义期末) 下列计算正确的是（　　）

A . a²+a⁴＝a⁶ B . （a²）³＝a⁵ C . a²•a³＝a⁵ D . a⁶÷a²＝a³

答案解析收藏纠错 + 选题
6. (2024八上·遵义期末) 一个多边形的内角和比它的外角和还大180°，这个多边形的边数为（　　）

A . 8 B . 7 C . 6 D . 5

答案解析收藏纠错 + 选题
7. (2024八上·遵义期末) 如图，已知AB＝AD ， AC＝AE ，要使△ABC≌△ADE ，则可以添加下列哪一个条件（　　）

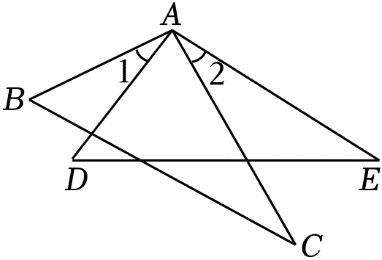
A . ∠1＝∠2 B . ∠B＝∠D C . ∠C＝∠E D . ∠BAC＝∠DAC

答案解析收藏纠错 + 选题
8. (2024八上·遵义期末) 如图，在△ABC中，∠ABC＝90°，沿BD折叠△BCD ，使点C恰好落在边AB上点E处，若∠A＝20°，则∠ADE的度数为（　　）

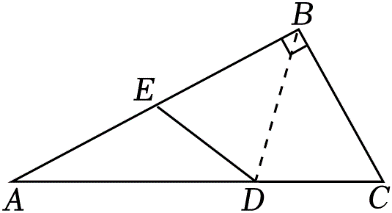
A . 70° B . 60° C . 55° D . 50°

答案解析收藏纠错 + 选题
9. (2024八上·遵义期末) 如图，已知∠AOB ，（1）以点O为圆心，任意长为半径画弧，分别交OA、OB于点C、D；（2）分别以点C、D为圆心，大于 $\text{[math]}$ CD的长为半径画弧，两弧在∠AOB的内部相交于点P；（3）画射线OP ．射线OP即为∠AOB的平分线．这样画出OP的依据是（　　）

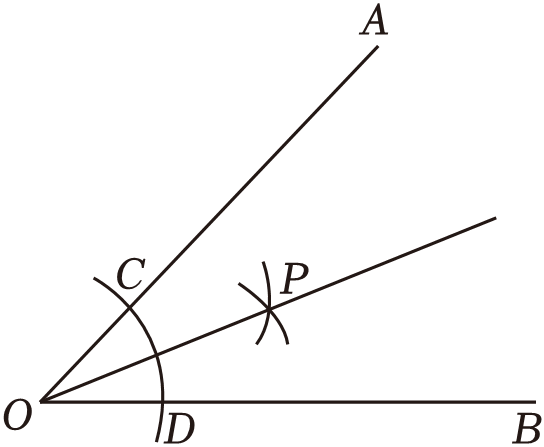
A . SAS ，全等三角形对应角相等 B . ASA ，全等三角形对应角相等 C . SSS ，全等三角形对应角相等 D . AAS ，全等三角形对应角相等

答案解析收藏纠错 + 选题
10. (2024八上·遵义期末) 某校计划在寒假中整修操场，已知甲队单独完成这项工程，刚好如期完工；乙队单独完成这项工程要比规定日期多用6天；学校决定甲、乙两队合作5天，余下的工程由乙队单独做，正好如期完成．设规定的工期为x天，根据题意列方程为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024八上·遵义期末) 如图，已知在△ABC中，AB＝AC ， ∠A＝120°，DE垂直平分AC ，若CD＝2，则BD的长为（　　）

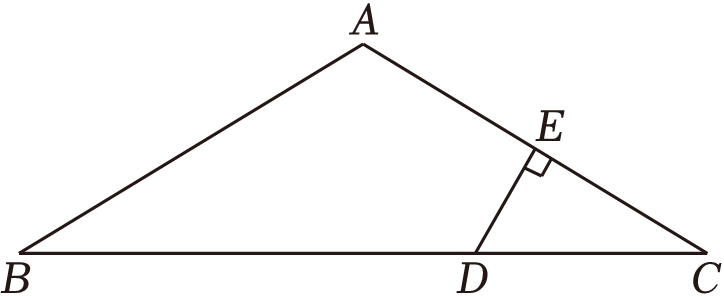
A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
12. (2024八上·遵义期末) 如图，点N在等边△ABC的边BC上，CN＝6，射线BD⊥BC ，垂足为点B ，点P是射线BD上一动点，点M是线段AC上一动点，当MP+NP的值最小时，CM＝7，则AC的长为（　　）

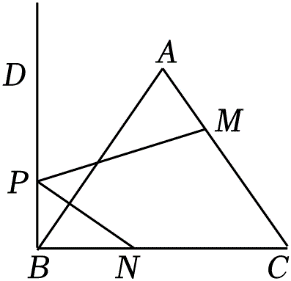
A . 8 B . 9 C . 10 D . 12

答案解析收藏纠错 + 选题

二、填空题（本题共4小题，每小题4分，共16分．请用黑色墨水笔或黑色签字笔将答案写在答颗卡上相应的位置．)

13. (2024八上·遵义期末) 若分式 $\text{[math]}$ 有意义，则x应满足的条件是．

答案解析收藏纠错 + 选题
14. (2024八上·遵义期末) 已知x﹣y＝4，xy＝6，则x²y﹣xy²＝．

答案解析收藏纠错 + 选题
15. (2024九下·武威模拟) 如图，在△ABC中，AB＝AC ， AD平分∠BAC ， DE⊥AB于点E ， BF⊥AC于点F ， DE＝1.3cm ，则BF＝cm ．

答案解析收藏纠错 + 选题
16. (2024九下·凉州模拟) 如图，在等边△ABC中，点D为AC的中点，点F在BC延长线上，点E在AB的延长线上，∠EDF＝120°，若BF＝9，BE＝2，则AC＝．

答案解析收藏纠错 + 选题

三、解答题（本题共9小题，共98分）

17. (2024八上·遵义期末)
1. （1）计算： $\text{[math]}$ ；
2. （2）解方程： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024九下·深圳月考) 先化简再求值 $\text{[math]}$ ，再从1，2，3中选取一个适当的数代入求值．

答案解析收藏纠错 + 选题
19. (2024八上·遵义期末) 某同学用10块高度都是5cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板ABD（∠ABD＝90°，BD＝BA），点B在CE上，点A和D分别与木墙的顶端重合．
1. （1）求证：△ACB≌△BED；
2. （2）求两堵木墙之间的距离．
答案解析收藏纠错 + 选题
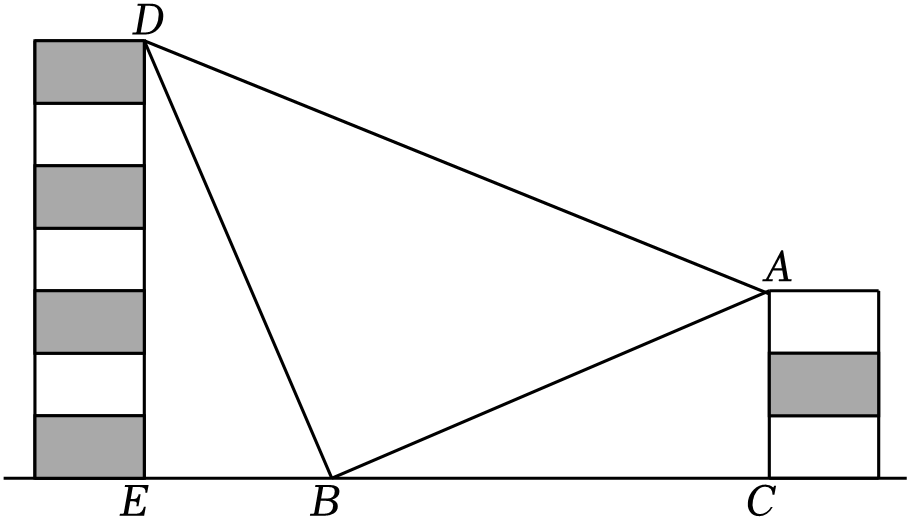
20. (2024八上·遵义期末) 图①，图②都是边长为1的3×3正方形网格，每个小正方形的顶点称为格点．点A、B、C均为格点，按下列要求画图：
1. （1）在图①中，画一条不与线段AB重合的线段MN ，使MN与AB关于某条直线对称（A、B的对应点分别为M、N），且M、N均为格点．
2. （2）在图②中，画一个△A₁B₁C₁ ，使△A₁B₁C₁与△ABC关于直线EF对称（A、B、C的对应点分别为A₁、B₁、C₁且A₁、B₁、C₁均为格点），再求出△A₁B₁C₁的面积．
答案解析收藏纠错 + 选题
21. (2024八上·遵义期末) 现有长为a ，宽为b的长方形卡片（如图①）若干张，某同学用4张卡片拼出了一个大正方形（不重叠、无缝隙，如图②）．
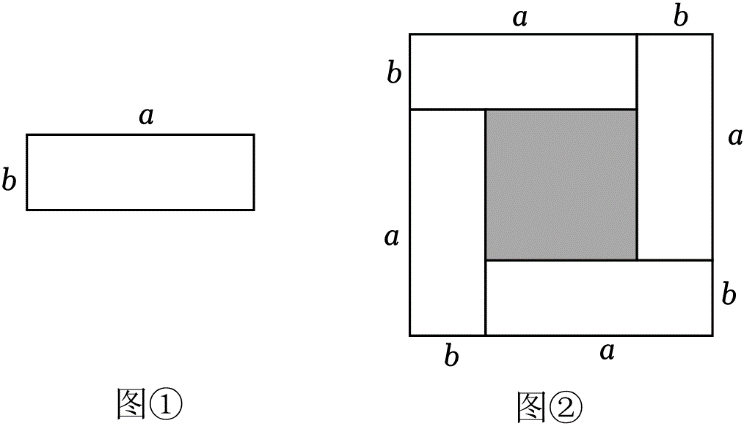
1. （1）图②中，大正方形的边长是，阴影部分正方形的边长是．（用含a ， b的式子表示）
2. （2）用两种方法表示图②中阴影部分正方形的面积（不化简），并用一个等式表示（a+b）² ，（a﹣b）² ， ab三者之间的数量关系．
3. （3）已知a+b＝8，ab＝7，求图②中阴影部分正方形的边长．
答案解析收藏纠错 + 选题
22. (2024八上·遵义期末) 遵义市某中学为了践行劳动课程标准和让学生体验农耕劳动，开辟了一处耕种园，需要采购一批菜苗开展种植活动．据调查：每捆A种菜苗，在市场上购买的价格是在菜苗基地处购买的1.5倍，用600元在市场上购买的A种菜苗数量比在菜苗基地购买数量的一半要多4捆．
1. （1）求菜苗基地每捆A种菜苗的价格．
2. （2）菜苗基地每捆B种菜苗的价格是35元，学校预计用不多于1960元的资金在菜苗基地购买A ， B两种菜苗共80捆，同时菜苗基地为支持该校活动，对A ， B两种菜苗均提供八折优惠．求至少可购买A种菜苗多少捆？
答案解析收藏纠错 + 选题
23. (2024八上·遵义期末) 如图，在△ABC中，∠BAC＝90°，AB＝AC ， DC⊥AC ，垂足为C ， AD交线段BC于F ， E是AC边上一点，连接BE ，交AD于点G且BE＝AD ．
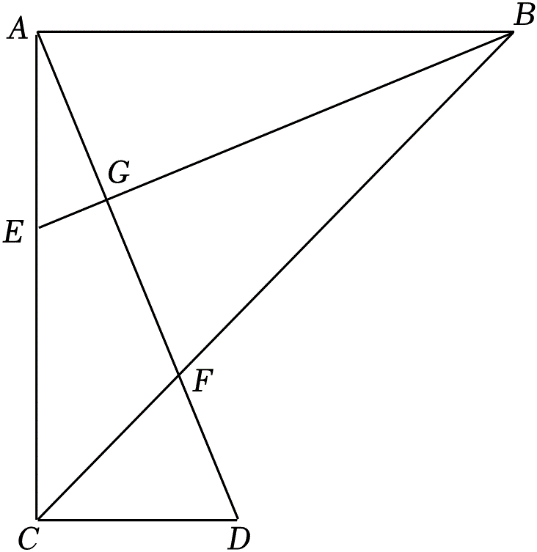
1. （1）猜猜BE与AD有怎样的位置关系？说说你的理由；
2. （2）若BE是∠ABC的角平分线，试说明△CFD是等腰三角形．
答案解析收藏纠错 + 选题
24. (2024八上·遵义期末) 阅读：换元法是一种重要的数学方法，是解决数学问题的有力工具．下面是对多项式（x²﹣2x）（x²﹣2x+2）+1进行因式分解的解题思路：将“x²﹣2x”看成一个整体，令x²﹣2x＝m ，则：原式＝m（m+2）+1＝m²+2m+1＝（m+1）² ．再将“m”还原为“x²﹣2x”即可．
解题过程如下：
解：设x²﹣2x＝m ，则：原式＝m（m+2）+1＝m²+2m+1＝（m+1）²＝（x²﹣2x+1）² ．
问题：
1. （1）以上解答过程并未彻底分解因式，请你直接写出最后的结果：；
2. （2）请你模仿以上方法，将多项式（x²+6x）（x²+6x+18）+81进行因式分解；
3. （3）换元法在因式分解、解方程、计算中都有广泛应用，请你模仿以上方法尝试计算：
  $\text{[math]}$
答案解析收藏纠错 + 选题
25. (2024八上·遵义期末) 在Rt△ABC中，∠ACB＝90°，AC＝BC ，点E为AC上一动点，过点A作AD⊥BE于D ，连接CD ．
1. （1）【观察发现】
  如图①，∠DAC与∠DBC的数量关系是；
2. （2）【尝试探究】
  点E在运动过程中，∠CDB的大小是否改变，若改变，请说明理由，若不变，求∠CDB的度数；
3. （3）【深入思考】
  如图②，若E为AC中点，探索BE与DE的数量关系．
答案解析收藏纠错 + 选题