题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /人教版（2024） /七年级下册 /第五章相交线与平行线 /本章复习与测试

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

2023-2024学年初中数学人教版七年级下学期第五章相...

更新时间：2024-03-15 浏览次数：177 类型：单元试卷

一、选择题

1. (2024七上·吴兴期末) 如图是小周同学在校运会上投掷实心球的场景，当投掷完毕时，测量员选取AB的长度作为小周的成绩，其依据是（）．

A . 垂线段最短 B . 两点之间线段最短 C . 两点确定一条直线 D . 过一点有且只有一条直线与已知直线垂直

答案解析收藏纠错 + 选题
2. (2023七上·龙川期末) 直线、线段、射线的位置如图所示，下图中能相交的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024八上·邵阳期末) 在下列命题中，是真命题的是（）

A . 相等的角是对顶角 B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 两个锐角的和是钝角 D . 有两个角相等的三角形是等腰三角形

答案解析收藏纠错 + 选题
4. (2024·惠城模拟) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ 的直角顶点A落在直线a上，点B落在直线b上，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的大小为（）

A . 50° B . 45° C . 40° D . 35°

答案解析收藏纠错 + 选题
5. (2024七上·榆树期末) 如图，下列条件中能判定 $\text{[math]}$ 是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. 如图，将网格中的三条线段沿网格线的方向(水平或竖直)平移后组成一个首尾依次相接的三角形，至少需要移动（）

A . 12格 B . 11格 C . 9 格 D . 8格

答案解析收藏纠错 + 选题
7. 下列图形中，周长最长的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2024七下·恩施期中) 如图，A，B，C，D中的哪幅图案可以通过图案①平移得到（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. 过直线l外一点P作直线l的平行线，下列尺规作图中，错误的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. 如图1，当光从空气进入水中时，会发生折射，满足入射角∠1 与折射角∠2 的度数比为4：3.如图2，在同一平面上，两条光线同时从空气进入水中，两条入射光线与水面的夹角分别为α，β，水中两条折射光线的夹角为γ，则α，β，γ三者之间的数量关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . α+β=γ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024八上·靖边期末) “平行于同一条直线的两条直线平行”是命题（填“真”或“假”）．

答案解析收藏纠错 + 选题
12. 如图1，一块长为a(cm)，宽为b(cm)的长方形地板中间有一条裂缝.如图2，若把裂缝右边的一块向右平移x(cm)，则产生的裂缝的面积为cm².

答案解析收藏纠错 + 选题
13. 如图，平面反光镜AC斜放在地面AB上，一束光线从地面上的P点射出，DE是反射光线.已知∠APD=120°，若要使反射光线DE∥AB，则∠CAB应调节为°(提示：∠ADP=∠CDE，三角形的内角和等于180°).

答案解析收藏纠错 + 选题
14. (2024七上·温州期末) 如图，直线AB，CD交于点O，∠AOC：∠COE=1：2．若∠BOD=28°，则∠COE等于度．

答案解析收藏纠错 + 选题
15. 如图，将长方形纸片 ABCD沿EF折叠后，点A，B分别落在A'，B'的位置，再沿AD边将∠A'折叠到∠H处，若∠1=52°，则∠AEF= ，∠FEH= .

答案解析收藏纠错 + 选题

三、作图题

16. (2023八上·浑江期末) 如图，已知直线l和l外一点P，用尺规作l的垂线，使它经过点P.（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题
17. 如图，在∠AOB 内有一点 P.
1. （1）过点 P 作l₁∥OA.
2. （2）过点 P 作l₂∥OB.
3. （3）用量角器量一量 l₁ 与 l₂ 的夹角与∠O 有怎样的数量关系?
答案解析收藏纠错 + 选题

四、解答题

18. (2024七上·吴兴期末) 如图，已知直线AB与CD相交于点O，OD平分∠BOE，∠AOE＝126°．
1. （1）求∠AOC的度数.
2. （2）若直线OF⊥OE，求∠DOF的度数.
答案解析收藏纠错 + 选题

五、实践探究题

19. (2024七上·长春汽车经济技术开发期末) 如图
1. （1）【感知】已知：如图①，点E在AB上，且CE平分∠ACD，∠1＝∠2．求证：AB∥CD．
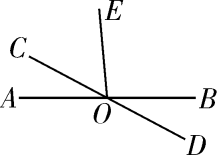
  将下列证明过程补充完整：
  证明：∵CE平分∠ACD（已知），
  ∴∠2＝∠    ▲        （角平分线的定义），
  ∵∠1＝∠2（已知），
  ∴∠1＝∠    ▲        （等量代换），
  ∴AB∥CD（      ）．
2. （2）【探究】已知：如图②，点E在AB上，且CE平分∠ACD，AB∥CD．求证：∠1＝∠2．
3. （3）【应用】如图③，BE平分∠DBC，点A是BD上一点，过点A作AE∥BC交BE于点E，∠ABC：∠BAE＝4：5，直接写出∠E的度数．
答案解析收藏纠错 + 选题
20. (2024七上·九台期末) 【教材呈现】如图是华师版七年级上册数学教材第176页的部分内容．有了“两直线平行，同位角相等”，我们就能用推理的方法得出“两条平行线被第三条直线所截，内错角相等”．
如图①，已知平行线a、b被直线l所截，我们将∠1的对顶角记为∠3．
1. （1）下面是“两直线平行，内错角相等”的推理过程，在括号内填写理由．
  ∵a∥b（      　），
  ∴∠2＝∠3（               　）．
  ∵∠1＝∠3（         　），
  ∴∠1＝∠2（        　）．
2. （2）【拓展应用】如图②，AB∥CD，BC∥DE，若∠B＝47°，则∠D＝°．
3. （3）如图③，已知AB∥CD，∠1＝∠2，试说明∠BEF＝∠EFC．
答案解析收藏纠错 + 选题
21. 小明完成作业后在家复习，他看到七下课本第12页例4，感到这个结论十分有趣，便尝试探究起来.
1. （1）【基础巩固】
  与例4条件和结论互换，改成了：“如图1，AP 平分∠BAC，CP平分∠ACD，AB∥CD，则∠1+∠2=90°，”小明认为这个结论正确，你赞同他的想法吗? 请说明理由.
2. （2）【尝试探究】
  小明发现：若将其中一条角平分线改成AC的垂线，则“∠1+∠2=90°”这个结论不成立.请帮小明完成探究：
  如图2，AB∥CD，AP平分∠BAC，CP⊥AC，∠1是AP与AB的夹角，∠2 是CP与CD的夹角.
  ①若∠2=22°，求∠1的度数.
  ②试说明：2∠1-∠2=90°.
3. （3）【拓展提高】
  如图3，若AB∥CD，AP⊥AC，CP平分∠ACD，请直接写出∠1与∠2的数量关系.
答案解析收藏纠错 + 选题

六、综合题

22. (2023七上·哈尔滨月考) 已知：点E在线段 $\text{[math]}$ 间（如图1）．连接 $\text{[math]}$ ． $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ．
2. （2）如图2，点F在点E右侧．连接 $\text{[math]}$ ．求证 $\text{[math]}$ ．
3. （3）如图3在（2）的条件下，线段 $\text{[math]}$ ， $\text{[math]}$ 的延长线交于点H ． $\text{[math]}$ 交 $\text{[math]}$ 于点K ．当 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
23. (2023七下·冷水滩期末) 如图1，已知两条直线 $\text{[math]}$ 被直线 $\text{[math]}$ 所截，分别交于点E，点F， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点M，且 $\text{[math]}$ ．
1. （1）判断直线 $\text{[math]}$ 与直线 $\text{[math]}$ 是否平行，并说明理由；
2. （2）如图2，点G是射线 $\text{[math]}$ 上一动点（不与点M，F重合）， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点H，过点H作 $\text{[math]}$ 于点N，设 $\text{[math]}$ ．
  ①当点G在点F的右侧时，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
  
  ②当点G在运动过程中， $\text{[math]}$ 和 $\text{[math]}$ 之间有怎样的数量关系？请写出你的猜想，并加以证明．
答案解析收藏纠错 + 选题

试卷信息