湖南省2024年初中学业水平考试模拟数学试卷

更新时间：2024-04-10 浏览次数：142 类型：中考模拟

一、选择题（在下列各题的四个选项中，只有一项是符合题意的. 请在答题卡中填涂符合题意的选项. 本大题共10个小题，每小题3分，共30分）

1. (2024·雅安) 2024的相反数是（　　）

A . 2024 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·湖南模拟) 某科学家研究发现人类头发的直径是 $\text{[math]}$ 分米 $\text{[math]}$ 将 $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·湖南模拟) 下列计算正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八上·宜州期末) 把一块直尺与一块三角板如图放置，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024·湖南模拟) “科学用眼，保护视力”是青少年珍爱生命的具体表现．某校随机抽查了50名八年级学生的视力情况，得到的数据如下表：
视力
4.7以下
4.7
4.8
4.9
4.9以上
人数
5
7
10
16
12
则本次调查中视力的众数和中位数分别是（）

A . 4.9和4.8 B . 4.9和4.9 C . 4.8和4.8 D . 4.8和4.9

答案解析收藏纠错 + 选题
6. (2024·湖南模拟) 如图，在直径为 $\text{[math]}$ 的 $\text{[math]}$ 中，弦 $\text{[math]}$ ， $\text{[math]}$ 于点C ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·南海月考) 如图，一次函数 $\text{[math]}$ 与x轴、y轴分别交于 $\text{[math]}$ 两点，则不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024·湖南模拟) 数学家斐波那契编写的《算经》中有如下分钱问题：第一次由一组人平分10元钱，每人分得若干，第二次比第一次增加6人，平分40元钱，则第二次每人分得的钱与第一次相同，设第二次分钱的人数为 $\text{[math]}$ 人，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
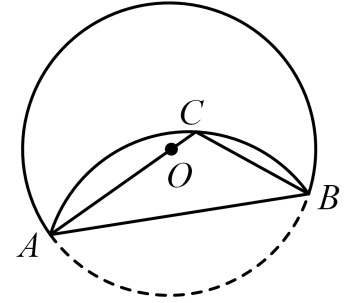
9. (2024·湖南模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 一条弦，将劣弧沿弦 $\text{[math]}$ 翻折，连结 $\text{[math]}$ 并延长交翻折后的弧于点 $\text{[math]}$ ，连结 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024·湖南模拟) P₁（x₁ ， y₁），P₂（x₂ ， y₂）是平面直角坐标系中的任意两点，我们把|x₁﹣x₂|+|y₁﹣y₂|叫做P₁ ， P₂两点间的“直角距离”，记作d（P₁ ， P₂）．比如：点P（2，﹣4），Q（1，0），则d（P ， Q）=|2﹣1|+|﹣4﹣0|=5，已知Q（2，1），动点P（x ， y）满足d（P ， Q）=3，且x、y均为整数，则满足条件的点P有（　　）个．

A . 4 B . 8 C . 10 D . 12

答案解析收藏纠错 + 选题

二、填空题（本大题共8小题，每小题3分，共24分）

11. (2024·湖南模拟) 若二次根式 $\text{[math]}$ 在实数范围内有意义，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
12. (2024九下·茂名月考) 分解因式：2x³－8x=.

答案解析收藏纠错 + 选题
13. (2024·湖南模拟) 在周长为800米的三角形地块中修建如图所示的三条水渠，则水渠总长为米．

答案解析收藏纠错 + 选题
14. (2024·湖南模拟) 如图，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于A ， B两点，过点A作 $\text{[math]}$ 轴，垂足为点M ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则k的值为．

答案解析收藏纠错 + 选题
15. (2024·湖南模拟) 有下列几个数： $\text{[math]}$ ， 0， $\text{[math]}$ ， 5，从这四个数中随机抽取一个数，恰好是一元二次方程 $\text{[math]}$ 的根的概率是．

答案解析收藏纠错 + 选题
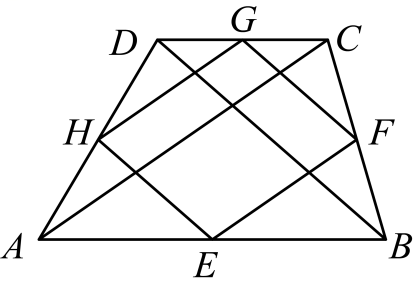
16. (2024·湖南模拟) 如图，点E ， F ， G ， H分别是四边形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点，连接四边形 $\text{[math]}$ 各边中点，当四边形 $\text{[math]}$ 满足条件，四边形 $\text{[math]}$ 是矩形．

答案解析收藏纠错 + 选题
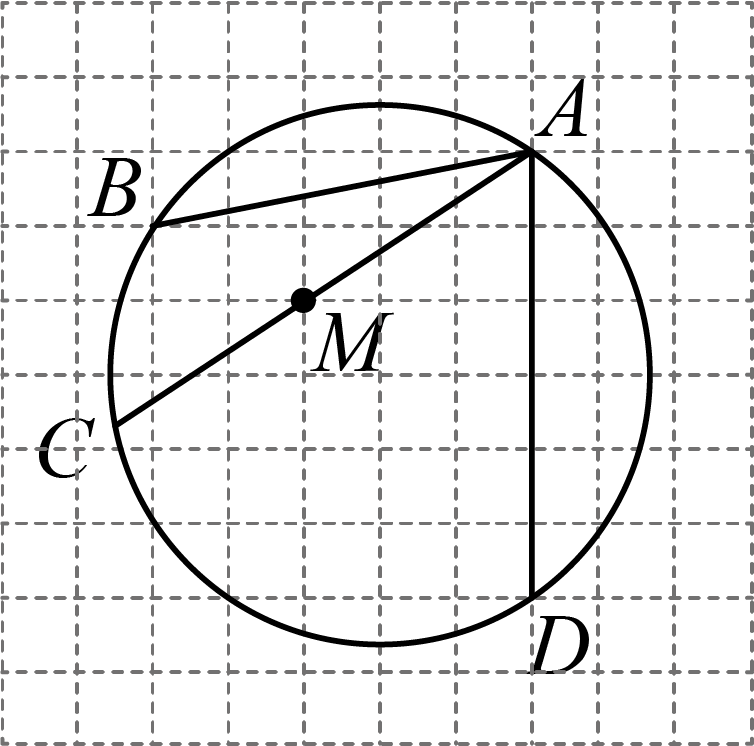
17. (2024·湖南模拟) 如图，在每个小正方形的边长为1的网格中，点A ，点B ，点D均在格点上，并且在同一个圆上，取格点M ，连接 $\text{[math]}$ 并延长交圆于点C ，连接 $\text{[math]}$ ．请在如图所示的网格中，用无刻度的直尺画出弦 $\text{[math]}$ ，使 $\text{[math]}$ 平分 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024·湖南模拟) 抛物线 $\text{[math]}$ 的部分图象如图所示，则方程 $\text{[math]}$ 的根是．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，第19-20题每小题6分，第21-22题每小题8分，第23-24题每小题9分，第25-26题每小题10分，共66分）

19. (2024·湖南模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2024·湖南模拟) 先化简 $\text{[math]}$ ，再从 $\text{[math]}$ ， $\text{[math]}$ ， 0，2中选择一个合适的数作为a的值代入求值．

答案解析收藏纠错 + 选题
21. (2024·湖南模拟) 体育是湖南省中考的必考科目，现随机抽取初二年级部分学生进行“你最想选择哪个考试科日？”的问卷调查，参与调查的学生需从A、B、C、D、E五个选项（A：引体向上；B：仰卧起坐；C：立定跳远；D：实心球：E：跳绳）中任选一项（必选且只选一项）．根据调查结果绘制了如下两幅不完整的统计图．
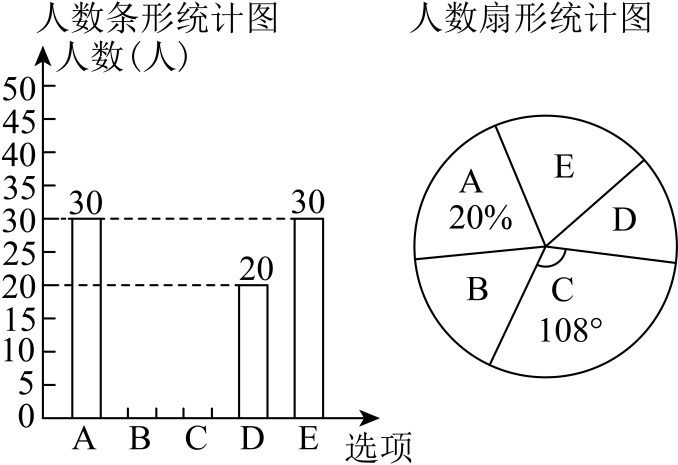
请根据图中提供的信息完成以下问题：
1. （1）参加本次调查的一共有名学生；在扇形统计图中，“D”所在扇形圆心角的度数是；
2. （2）请你补全条形统计图；
3. （3）已知某中学初二年级共有750名学生，请你根据调查结果，估计初二年级最想选择“跳绳”的学生有多少人？
答案解析收藏纠错 + 选题
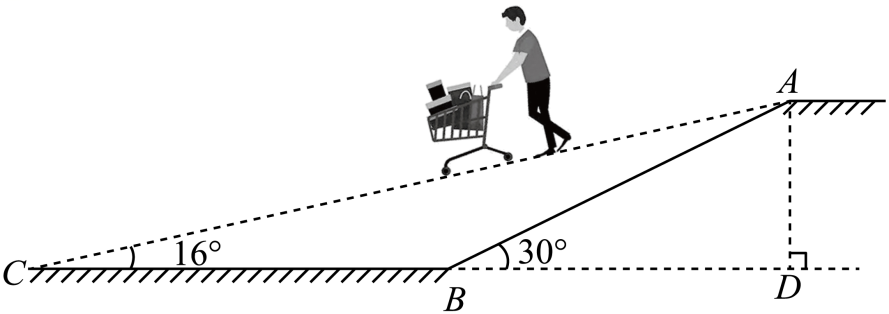
22. (2024·湖南模拟) 某商场从安全和便利的角度出发，为提升顾客的购物体验，准备将自动扶梯由原来的阶梯式改造成斜坡式，如图，已知商场的层高 $\text{[math]}$ 为 $\text{[math]}$ ，坡角 $\text{[math]}$ 为 $\text{[math]}$ ，改造后的斜坡式自动扶梯的坡角 $\text{[math]}$ ，请你计算改造后的自动扶梯增加的占地长度 $\text{[math]}$ 的长．（结果精确到 $\text{[math]}$ ，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
23. (2024·湖南模拟) 我区启动“绿色公园”建设，计划对面积为 $\text{[math]}$ 的区域进行绿化，经投标由甲、乙两个工程队来完成，已知甲工程队完成绿化 $\text{[math]}$ 的面积与乙工程队完成绿化 $\text{[math]}$ 的面积所用的时间相同，若甲工程队每天比乙工程队多绿化 $\text{[math]}$ ．
1. （1）求甲、乙两工程队每天各能完成多少面积的绿化；
2. （2）若甲工程队每天的绿化费用是 $\text{[math]}$ 万元，乙工程队每天的绿化费用是 $\text{[math]}$ 万元，要使这次绿化的总费用不超过30万元，则至少应安排乙工程队绿化多少天？
答案解析收藏纠错 + 选题
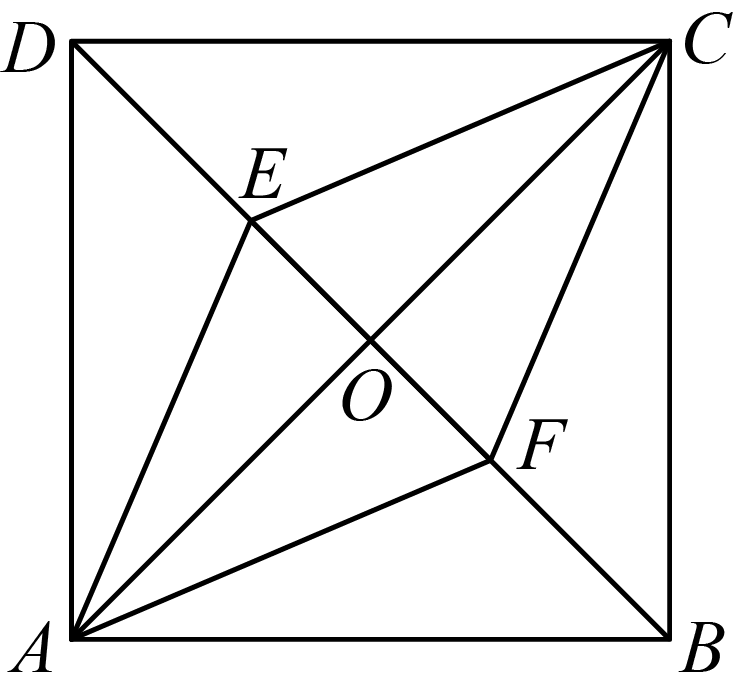
24. (2024·湖南模拟) 如图，四边形 $\text{[math]}$ 是菱形，对角线 $\text{[math]}$ 、 $\text{[math]}$ 交于点O ，点D、B是对角线 $\text{[math]}$ 所在直线上两点，且 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是正方形：
2. （2）若四边形 $\text{[math]}$ 的面积为72， $\text{[math]}$ ，求点F到线段 $\text{[math]}$ 的距离．
答案解析收藏纠错 + 选题
25. (2024·湖南模拟) 已知四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，直径 $\text{[math]}$ 于点F ．
1. （1）如图1，求证： $\text{[math]}$ ；
2. （2）如图2，连接 $\text{[math]}$ ，若 $\text{[math]}$ 平分 $\text{[math]}$ ，过点D作 $\text{[math]}$ 于点H ，求证： $\text{[math]}$ ；
3. （3）如图3，在（2）的条件下，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点G ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
26. (2024·湖南模拟) 已知抛物线 $\text{[math]}$ ，其中 $\text{[math]}$ 是实数．
1. （1）已知三个点 $\text{[math]}$ ，其中有一个点是抛物线的顶点，请选出该点并求抛物线的解析式；
2. （2）在（1）的条件下，抛物线与 $\text{[math]}$ 轴交于 $\text{[math]}$ 两点（点 $\text{[math]}$ 在 $\text{[math]}$ 轴正半轴），与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，抛物线的顶点的记为 $\text{[math]}$ ，
  ①若点 $\text{[math]}$ 在点 $\text{[math]}$ 之间的抛物线上运动（不与点 $\text{[math]}$ 重合），连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．记 $\text{[math]}$ 的面积分别为 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值；
  ②过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与抛物线的另一个交点为 $\text{[math]}$ ，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，交抛物线于点 $\text{[math]}$ ，过 $\text{[math]}$ 的中点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ．求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题