江西省南昌市2023-2024学年九年级上学期期末数学试题

更新时间：2024-05-30 浏览次数：28 类型：期末考试

一、选择题（本大题共6小题，每小题3分，共18分）每小题给出的四个选项中，只有一项是正确的，请将正确选项的代号填涂在答题卡上.

1. (2024九上·南昌期末) 如图，是由 $\text{[math]}$ 个棱长均为 $\text{[math]}$ 的正方体组成的几何体，它的左视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·南昌期末) 下列事件是不可能事件的是（）

A . 太阳从东方升起 B . 三条线段组成一个三角形 C . $\text{[math]}$ （ $\text{[math]}$ 为实数） D . 购买一张大乐透，中奖500万

答案解析收藏纠错 + 选题
3. (2024九上·南昌期末) 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的直径，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·南昌期末) 如图，在平面直角坐标系中，已知点E(−4，2)，F(−1，−1).以原点O为位似中心，把△EFO扩大到原来的2倍，则点E的对应点E′的坐标为（）

A . (−8，4) B . (8，−4) C . (8，4)或(−8，−4) D . (−8，4)或(8，−4)

答案解析收藏纠错 + 选题
5. (2024九上·南昌期末) 如图，在4×4的正方形网格中，每个小正方形的顶点称为格点，左上角阴影部分是一个以格点为顶点的正方形（简称格点正方形）.若再作一个格点正方形，并涂上阴影，使这两个格点正方形无重叠，且组成的图形既是轴对称图形，又是中心对称图形，则这个格点正方形的作法共有（）

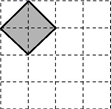
A . 2种 B . 3种 C . 4种 D . 5种

答案解析收藏纠错 + 选题
6. (2024九上·南昌期末) 用绘图软件绘制出函数 $\text{[math]}$ 的图象，如图，则根据你学习函数图象的经验，下列对a、b大小的判断，正确的是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

7. (2024九上·南昌期末) 已知 $\text{[math]}$ 两点，若 $\text{[math]}$ 两点关于原点对称，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
8. (2024九下·上海市模拟) 一个不透明的口袋里装有若干除颜色外其他完全相同的小球，其中有6个黄球，将口袋中的球摇匀，从中任意摸出一个球记下颜色后再放回，通过大量重复上述试验后发现，摸到黄球的频率稳定在30%，由此估计口袋中共有小球个.

答案解析收藏纠错 + 选题
9. (2024九上·南昌期末) “南昌之星”摩天轮，位于江西省南昌市红谷滩新区红角洲赣江边上的赣江市民公园，摩天轮高160m（最高点到地面的距离）．如图，点O是摩天轮的圆心，AB是其垂直于地面的直径，小贤在地面点C处利用测角仪测得摩天轮的最高点A的仰角为45°，测得圆心O的仰角为30°，则摩天轮的半径为m ．（结果保留根号）

答案解析收藏纠错 + 选题
10. (2024九上·南昌期末) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上一点，且 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，若 $\text{[math]}$ 的面积是 $\text{[math]}$ ，则 $\text{[math]}$ 的面积是．

答案解析收藏纠错 + 选题
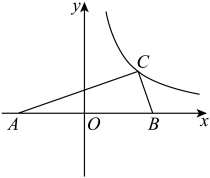
11. (2024九上·南昌期末) 如图，直角坐标系原点为 $\text{[math]}$ 斜边的中点， $\text{[math]}$ ， $\text{[math]}$ 点坐标为 $\text{[math]}$ ，且 $\text{[math]}$ ，反比例函数 $\text{[math]}$ 经过点C，则k的值为．

答案解析收藏纠错 + 选题
12. (2024九上·南昌期末) 如图，在半径为1的⊙O中，直线l为⊙O的切线，点A为切点，弦AB=1，点P在直线l上运动，若△PAB为等腰三角形，则线段OP的长为．

答案解析收藏纠错 + 选题

三、解答题（本大题共5小题，每小题6分，共30分）

13. (2024九上·南昌期末) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2024九上·南昌期末) 如图，l₁∥l₂∥l₃ ， AB＝5，DE＝4，EF＝8，求AC的长．

答案解析收藏纠错 + 选题
15. (2024九上·南昌期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转角 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长度；
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
16. (2024九上·南昌期末) 如图，已知反比例函数 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ 的图象与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 两点分别在 $\text{[math]}$ 轴和 $\text{[math]}$ 轴的正半轴上， $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ ．
1. （1）求反比例函数的解析式；
2. （2）求直线 $\text{[math]}$ 的表达式和 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
17. (2024九上·南昌期末) 为了响应国家中小学生“课后服务”的政策．江西某学校结合学校实际课后情况开设了四门课程供学生选择．四门课程分别是A：快乐阅读；B：趣味数学；C：轻松英语；D：开心书法．学生需要从中选两门课程．
1. （1）七年级学生小真第一次选择了课程A ，如果她从其他三门学科中再选择一门课程，则她抽到课程C的概率是；
2. （2）七年级学生小美从四门课程中抽取两门课程进行学习，请用树状图法，求恰好选中B和D两门课程的概率．
答案解析收藏纠错 + 选题
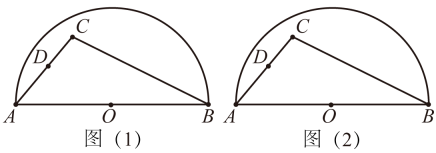
18. (2024九上·南昌期末) 如图，点C是以AB为直径的半圆O内任意一点，连接AC，BC，点D在AC上，且AD＝CD，请仅用无刻度的直尺分别按下列要求画图（保留画图痕迹）．
1. （1）在图（1）中，画出 $\text{[math]}$ 的中线AE；
2. （2）在图（2）中，画出 $\text{[math]}$ 的角平分线AF．
答案解析收藏纠错 + 选题

四、解答题（本大题共3小题，每小题8分，共24分）

19. (2024九上·南昌期末) 盒中有x枚黑棋和y枚白棋，这些棋除颜色外无其他差别．
1. （1）从盒中随机取出一枚棋子，如果它是黑棋的概率是 $\text{[math]}$ ，写出表示x和y关系的表达式．
2. （2）往盒中再放进10枚黑棋，取得黑棋的概率变为 $\text{[math]}$ ，求x和y的值．
答案解析收藏纠错 + 选题
20. (2024九上·南昌期末) 如图，直线 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴， $\text{[math]}$ 轴依次交于点B，点C．
1. （1）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
2. （2）判定 $\text{[math]}$ 与 $\text{[math]}$ 的比值能否与 $\text{[math]}$ 相等？若有，求线段 $\text{[math]}$ 的长度；若没有，请说明理由．
答案解析收藏纠错 + 选题
21. (2024九上·南昌期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上的动点，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 的长为半径作圆交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ 上的点，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 与点 $\text{[math]}$ 恰好重合．
1. （1）如图1，若 $\text{[math]}$ ，证明 $\text{[math]}$ 与直线 $\text{[math]}$ 相切；
2. （2）如图2，若 $\text{[math]}$ 经过点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
  ① $\text{[math]}$ 的长是 ▲ ；
  ②判断四边形 $\text{[math]}$ 的形状，并证明．
答案解析收藏纠错 + 选题

五、解答题（本大题共2小题，每小题9分，共18分）

22. (2024九上·南昌期末) 图1是一款厨房常用的防烫取盘器，图2是其侧面示意图．经测量：支架 $\text{[math]}$ ，托盘器外沿 $\text{[math]}$ ．支架 $\text{[math]}$ 可绕点A转动， $\text{[math]}$ ．经调研发现，当 $\text{[math]}$ 时，操作人员手势自然．
（参考数据 $\text{[math]}$ ， $\text{[math]}$ ）
1. （1）当点D和点E重合时，求 $\text{[math]}$ 的度数；
2. （2）若一圆形盘盘口的直径为 $\text{[math]}$ ，请判断此时操作人员用该取盘器手势是否自然；
3. （3）当 $\text{[math]}$ 时，请计算点A到 $\text{[math]}$ 的距离．
答案解析收藏纠错 + 选题
23. (2024九上·南昌期末) 如图
1. （1）课本再现：如图1， $\text{[math]}$ 是 $\text{[math]}$ 的一个外角，写出 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 的数量关系
2. （2）类比探究：如图2， $\text{[math]}$ 是 $\text{[math]}$ 与 $\text{[math]}$ 的公共边， $\text{[math]}$ ， $\text{[math]}$ ．
  ① $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是 ▲ ；
  ②求证 $\text{[math]}$
3. （3）拓展应用：如图3，点D是正方形 $\text{[math]}$ 内一点，且在以O 为圆心， $\text{[math]}$ 为半径的圆弧上，若 $\text{[math]}$ ， $\text{[math]}$ ，直接写出线段 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题

六、解答题（本大题共1小题，共12分）

24. (2024九上·南昌期末) 如图
图1 图2 图3
1. （1）【特例感知】如图 $\text{[math]}$ ，点 $\text{[math]}$ 是正方形 $\text{[math]}$ 对角线 $\text{[math]}$ 上一点， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ .
  ①求证：四边形 $\text{[math]}$ 是正方形；
  ② $\text{[math]}$ = ▲ ；
2. （2）【规律探究】将正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转得到图 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
  $\text{[math]}$ 的比值是否会发生变化？说明理由；
3. （3）【拓展应用】如图 $\text{[math]}$ ，在图 $\text{[math]}$ 的基础上，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点；四边形 $\text{[math]}$ 是否是正方形？说明理由.
答案解析收藏纠错 + 选题