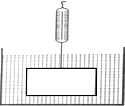
 B .
B . 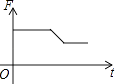 C .
C . 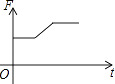 D .
D . 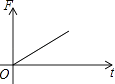
①点O到直线BE的距离为;②OE的长为
;③AB=AE;④直线AE的解析
式为y=x+
+1.其中正确的是( )




|
求直线 第一步,在直线 第二步,将点 第三步,设直线 |
若将直线
向左平移
个单位长度,则平移后的直线解析式为 ;
若先将直线
向右平移
个单位长度,再向下平移
个单位长度,得到直线
, 则直线
的解析式为 .
已知一次函数的图象与直线
关于
轴对称,求一次函数的解析式;
若一次函数
的图象绕点
逆时针旋转
后得到直线
, 则直线
的解析式为 ▲ .
当直线
与线段
有交点时,求
的取值范围.
已知点
是直线
上一点,其横坐标为
过点
作直线
轴,将直线
在直线
下方部分记作
, 在直线
上及其上方的部分记为
, 将
沿直线
向上翻折得到
,
和
两部分组成的图象记为
当图象
与线段
四有一个公共点时,直接写出
的取值范围.
