 B .
B .  C .
C . 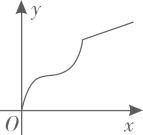 D .
D . 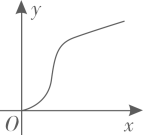
 B .
B . 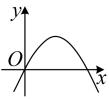 C .
C .  D .
D . 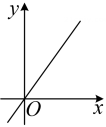
 B .
B .  C .
C .  D .
D . 
轿车行驶的路程 | 0 | 100 | 200 | 300 | 400 | … |
油箱剩余油量 | 50 | 42 | 34 | 26 | 18 | … |
下列说法不正确的是( )
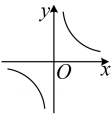
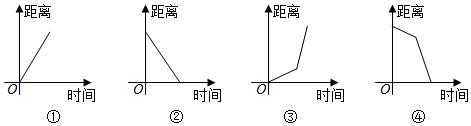
①如图1,货车匀速通过隧道(隧道长大于货车长),货车在隧道内的长度y与从车头进入隧道至车尾离开隧道的时间x;
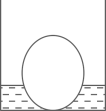
②如图2,实线是王大爷从家出发匀速散步行走的路线(圆心O表示王大爷家的位置),他离家的距离y与散步的时间x;
③如图3,往空杯中匀速倒水,倒满后停止,一段时间后,再匀速倒出杯中的水,杯中水的体积y与所用时间x

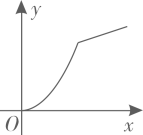
其中,变量y与x之间的函数关系大致符合下图的是( )

 B .
B .  C .
C .  D .
D . 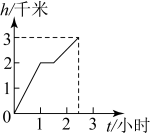

|
提出概念所用时间(x) |
2 |
5 |
7 |
10 |
12 |
13 |
14 |
17 |
20 |
|
对概念的接受能力(y) |
47.8 |
53.5 |
56.3 |
59 |
59.8 |
59.9 |
59.8 |
58.3 |
55 |
|
游泳次数 |
10 |
15 |
20 |
… |
x |
|
方式一的总费用(元) |
150 |
175 |
|
… |
|
|
方式二的总费用(元) |
90 |
135 |
|
… |
|
①求y与x之间的函数关系式;
②小明选择哪种方式比较合算?

|
海拔高度h(千米) |
0 |
1 |
2 |
3 |
4 |
5 |
… |
|
气温t(℃) |
20 |
14 |
8 |
2 |
|
|
根据上表,回答以下问题:

①飞机在2千米高空水平面上大约盘旋了 ▲ 分钟;
②挡风玻璃在高空爆裂,机长在高空经历了很大的艰险.求当时飞机所处高空的气温为多少摄氏度?


C | D | E | F | |
边上的点数x | 4 | 8 | 8 | 9 |
多边形面积S | 2 | 4 | 4 |
请完成表格,并归纳S与x之间的关系式为:.

图1 | 图2 | |
边上的点数x | ||
多边形面积S |
归纳S与x之间的关系式为: ▲ .
