湖南省长沙外国语学校2023-2024学年高二下学期3月月考...

更新时间：2024-07-11 浏览次数：16 类型：月考试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2024高三上·成都月考) 已知集合P＝{x|1＜x＜4}，Q＝{x|2＜x＜3}，则P∩Q＝（）

A . {x|1＜x≤2} B . {x|2＜x＜3} C . {x|3≤x＜4} D . {x|1＜x＜4}

答案解析收藏纠错 + 选题
2. (2024高二下·长沙月考) 若向量 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （　　）

A . 5 B . 8 C . 10 D . 12

答案解析收藏纠错 + 选题
3. (2024高二下·长沙月考) 设点 $\text{[math]}$ 是椭圆 $\text{[math]}$ 上的一点， $\text{[math]}$ 是椭圆的两个焦点，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高二下·长沙月考) 4名男生2名女生排成一排，要求两名女生排在一起的排法总数为（）

A . 48 B . 96 C . 120 D . 240

答案解析收藏纠错 + 选题
5. (2024高二下·大名月考) 某单位开展主题为“学习强国，我学习我成长”的知识竞赛活动，甲选手答对第一道题的概率为 $\text{[math]}$ ，连续答对两道题的概率为 $\text{[math]}$ .用事件A表示“甲选手答对第一道题”，事件B表示“甲选手答对第二道题”，则 $\text{[math]}$ ＝（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
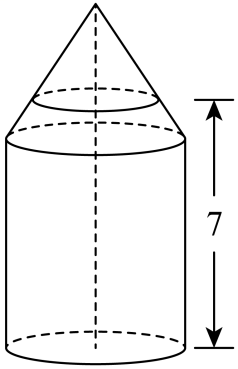
6. (2024高二下·长沙月考) 如图，一个装有水的密封瓶子，其内部可以看成由一个圆锥和一个圆柱组合而成的几何体，圆柱和圆锥的底面半径均为3，圆柱的高为6，圆锥的高为3，已知液面高度为7，则瓶子中水的体积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高二下·长沙月考) $\text{[math]}$ 年 $\text{[math]}$ 月 $\text{[math]}$ 日，阿贝尔奖和菲尔兹奖双料得主，英国 $\text{[math]}$ 岁高龄著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想，这一事件引起了数学界的震动.在 $\text{[math]}$ 年，德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题，也就是著名的黎曼猜想.在此之前著名的数学家欧拉也曾研究过这个何题，并得到小于数字 $\text{[math]}$ 的素数个数大约可以表示为 $\text{[math]}$ 的结论.若根据欧拉得出的结论，估计 $\text{[math]}$ 以内的素数个数为（）（素数即质数， $\text{[math]}$ ，计算结果取整数）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高二下·遂宁月考) 现将《西游记》、《红楼梦》、《水浒传》、《三国演义》、《史记》、《资治通鉴》6本不同的书籍分发给甲乙丙3人，每人至少分得1本，已知《西游记》分发给了甲，则不同的分发方式种数是（）

A . 180 B . 150 C . 120 D . 210

答案解析收藏纠错 + 选题

二、选择题:本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分.

9. (2024高二下·长沙月考) 已知复数 $\text{[math]}$ （ $\text{[math]}$ 是虚数单位），则下列命题中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ 的复平面上对应点在第二象限 C . $\text{[math]}$ D . $\text{[math]}$ 的虚部为 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高二下·龙马潭期末) 已知 $\text{[math]}$ 的展开式中，各项的二项式系数之和为128，则（）

A . $\text{[math]}$ B . 只有第4项的二项式系数最大 C . 各项系数之和为1 D . $\text{[math]}$ 的系数为560

答案解析收藏纠错 + 选题
11. (2024高二下·长沙月考) 古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状，把数分成许多类，如图中第一行图形中黑色小点个数：1，3，6，10，…称为三角形数，第二行图形中黑色小点个数：1，4，9，16，…称为正方形数，记三角形数构成数列 $\text{[math]}$ ，正方形数构成数列 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ B . 1225既是三角形数，又是正方形数 C . $\text{[math]}$ D . $\text{[math]}$ ，总存在 $\text{[math]}$ ，使得 $\text{[math]}$ 成立

答案解析收藏纠错 + 选题

三、填空题:本题共3小题，每小题5分，共15分.

12. (2024高二下·长沙月考) 若函数 $\text{[math]}$ 在 $\text{[math]}$ 处取得极值，则实数a的值为．

答案解析收藏纠错 + 选题
13. (2024高二下·长沙月考) 已知抛物线： $\text{[math]}$ ，焦点为 $\text{[math]}$ ，若 $\text{[math]}$ 在抛物线上且在第一象限， $\text{[math]}$ $\text{[math]}$ ，求直线 $\text{[math]}$ 的斜率为．

答案解析收藏纠错 + 选题
14. (2024高二下·长沙月考) 在一个抽奖游戏中，主持人从编号为1、2、3、4外观相同的空箱子中随机选择一个，放入一件奖品，再将箱子关闭，也就是主持人知道奖品在哪个箱子里，当抽奖人选择了某个箱子后，在箱子打开之前，主持人先随机打开另一个没有奖品的箱子，并问抽奖人是否愿意更改选择.现在已知甲选择了1号箱，若用 $\text{[math]}$ 表示i号箱有奖品 $\text{[math]}$ ，用 $\text{[math]}$ 表示主持人打开i号箱子 $\text{[math]}$ ，则 $\text{[math]}$ ； $\text{[math]}$ .

答案解析收藏纠错 + 选题

四、解答题:本题共5小题，共77分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.

15. (2024高二下·长沙月考) 在 $\text{[math]}$ 中，内角 $\text{[math]}$ 所对的边分别为 $\text{[math]}$ .已知 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ 的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 的周长.
答案解析收藏纠错 + 选题
16. (2024高二下·长沙月考) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上．
1. （1）求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ ，以及数列 $\text{[math]}$ 通项公式；
2. （2）若数列 $\text{[math]}$ 满足： $\text{[math]}$ ，设数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题
17. (2024高二下·长沙月考) 如图，在四棱锥 $\text{[math]}$ 中，平面 $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）若直线 $\text{[math]}$ 与底面 $\text{[math]}$ 所成的角的正切值为 $\text{[math]}$ ，求二面角 $\text{[math]}$ 的正切值．
答案解析收藏纠错 + 选题
18. (2024高二下·盐田月考) 已知函数 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 有极大值 $\text{[math]}$ .
1. （1）求实数 $\text{[math]}$ 的值；
2. （2）当 $\text{[math]}$ 时，证明： $\text{[math]}$ .
答案解析收藏纠错 + 选题
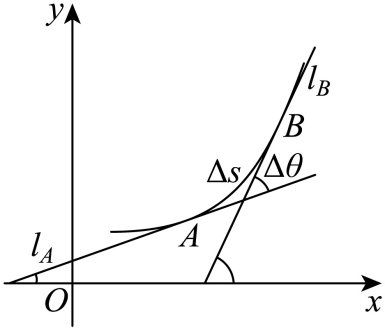
19. (2024高二下·长沙月考) 在几何学常常需要考虑曲线的弯曲程度，为此我们需要刻画曲线的弯曲程度．考察如图所示的光滑曲线C： $\text{[math]}$ 上的曲线段 $\text{[math]}$ ，其弧长为 $\text{[math]}$ ，当动点从A沿曲线段 $\text{[math]}$ 运动到B点时，A点的切线 $\text{[math]}$ 也随着转动到B点的切线 $\text{[math]}$ ，记这两条切线之间的夹角为 $\text{[math]}$ （它等于 $\text{[math]}$ 的倾斜角与 $\text{[math]}$ 的倾斜角之差）．显然，当弧长固定时，夹角越大，曲线的弯曲程度就越大；当夹角固定时，弧长越小则弯曲程度越大，因此可以定义 $\text{[math]}$ 为曲线段 $\text{[math]}$ 的平均曲率；显然当B越接近A ，即 $\text{[math]}$ 越小，K就越能精确刻画曲线C在点A处的弯曲程度，因此定义 $\text{[math]}$ （若极限存在）为曲线C在点A处的曲率．（其中y＇，y＇＇分别表示 $\text{[math]}$ 在点A处的一阶、二阶导数）
1. （1）求单位圆上圆心角为60°圆弧的平均曲率；
2. （2）求椭圆 $\text{[math]}$ 在 $\text{[math]}$ 处的曲率；
3. （3）定义 $\text{[math]}$ 为曲线 $\text{[math]}$ 的“柯西曲率”．已知在曲线 $\text{[math]}$ 上存在两点 $\text{[math]}$ 和 $\text{[math]}$ ，且P ， Q处的“柯西曲率”相同，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题