浙江省初中名校发展共同体2024年九年级下学期数学中考模拟试...

更新时间：2024-05-08 浏览次数：188 类型：中考模拟

一、选择题（本题有10小题，每题3分，共30分。每小题列出的四个备选项中只有一个是符合题目要求

1. 计算﹣2﹣8的结果是（）

A . ﹣6 B . ﹣10 C . 10 D . 6

答案解析收藏纠错 + 选题
2. 据科学家估计，地球的年龄大约是4600000000年，将数据4600000000用科学记数法表示应为（）

A . 0.46×10¹⁰ B . 4.6×10⁹ C . 46×10⁸ D . 4.6×10⁸

答案解析收藏纠错 + 选题
3. 如图所示几何体的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. 高速公路是指专供汽车高速行驶的公路．高速公路在建设过程中，通常要从大山中开挖隧道穿过，把道路取直以缩短路程．其中的数学原理是（）

A . 两点之间线段最短 B . 两点确定一条直线 C . 平行线之间的距离最短 D . 平面内经过一点有无数条直线

答案解析收藏纠错 + 选题
5. 下列函数中，函数值y随x的增大而减小的是（）

A . y＝6x B . y＝﹣6x C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. 若a＞b ，则下列不等关系一定成立的是（）

A . a+c＞b+c B . a﹣c＜b﹣c C . ac＞bc D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 从某个月的月历表中取一个2×2方块．已知这个方块所围成的4个方格的日期之和为44，求这4个方格中的日期．若设左上角的日期为x ，则下列方程正确的是（）

A . x+（x+1）+（x+7）+（x+14）＝44 B . x+（x+1）+（x+6）+（x+12）＝44 C . x+（x+1）+（x+7）+（x+8）＝44 D . x+（x+1）+（x+6）+（x+7）＝44

答案解析收藏纠错 + 选题
8. 如图，在 Rt△ABC中，∠ACB＝90°，CD为AB边上的高线，设∠A ， ∠B ， ∠ACB所对的边分别为a ， b ， c ，则（）

A . c＝bcosA+asinB B . c＝bsinA+asinB C . c＝bsinA+acosB D . c＝bcosA+acosB

答案解析收藏纠错 + 选题
9. 关于二次函数y＝a（x﹣1）（x﹣3）+2（a＜0）的下列说法中，正确的是（）

A . 无论a取范围内的何值，该二次函数的图象都经过（1，0）和（3，0）这两个定点 B . 当x＝2时，该二次函数取到最小值 C . 将该二次函数的图象向左平移1个单位，则当x＜0或x＞2时，y＜2 D . 设该二次函数与x轴的两个交点的横坐标分别为m ， n（m＜n），则1＜m＜n＜3

答案解析收藏纠错 + 选题
10. 如图，AB是⊙O的直径，弦CD⊥AB于点E ，在BC上取点F ，使得CF＝CE ，连结AF交CD于点G ，连结AD ．若CG＝GF ，则 $\text{[math]}$ 的值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每题3分，共18分）

11. 分解因式：mx²﹣m＝．

答案解析收藏纠错 + 选题
12. 盒中有m枚黑棋和n枚白棋，这些棋除颜色外无其它差别．从盒中随机取出一枚棋子，如果它是黑棋的概率是 $\text{[math]}$ ，则m关于n的关系表达式为．

答案解析收藏纠错 + 选题
13. 如图，直线m ， n被一组平行线a ， b ， c所截．若 $\text{[math]}$ ，则 $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
14. 已知△ABC的外接圆的半径为6，若∠A＝45°，∠B＝30°，则AB的长为．

答案解析收藏纠错 + 选题
15. 若a＝2﹣b ， ab＝t﹣1，则（a²﹣1）（b²﹣1）的最小值为．

答案解析收藏纠错 + 选题
16. 如图，在等腰Rt△ABC中，∠ACB＝90°，若点E ， F分别在边AC和边BC上，沿直线EF将△CEF翻折，使点C落于△ABC所在平面内，记为点D ．直线CD交AB于点G ．
1. （1）若CF落在边AB上，则 $\text{[math]}$ ＝；
2. （2）若 $\text{[math]}$ ，则tan∠CEF＝（用含的代数式表示）．
答案解析收藏纠错 + 选题

三、解答题（本题有8小题，共72分）

17. (2016·杭州) 计算6÷（﹣ $\text{[math]}$ ），方方同学的计算过程如下，原式=6 $\text{[math]}$ +6 $\text{[math]}$ =﹣12+18=6．请你判断方方的计算过程是否正确，若不正确，请你写出正确的计算过程．

答案解析收藏纠错 + 选题
18. 端午节是中国的传统节日，民间有端午节吃粽子的习俗，在端午节来临之际，某校七、八年级开展了一次“包粽子”实践活动，对学生的活动情况按10分制进行评分，成绩（单位：分）均为不低于6的整数、为了解这次活动的效果，现从这两个年级各随机抽取10名学生的活动成绩作为样本进行活整理，并绘制统计图表，部分信息如表：
八年级10名学生活动成绩统计表
成绩/分
6
7
8
9
10
人数
1
2
a
b
2
已知八年级10名学生活动成绩的中位数为8.5分．
请根据以上信息，完成下列问题：
1. （1）样本中，七年级活动成绩为7分的学生数是，七年级活动成绩的众数为分；
2. （2） a＝，b＝；
3. （3）若认定活动成绩不低于9分为“优秀”，根据样本数据，判断本次活动中优秀率高的年级是否平均成绩也高，并说明理由．
答案解析收藏纠错 + 选题
19. 如图，在△ABC中，AB＞AC ，点D在AB边上，点E在AC边上（点E不与A ， C重合），且∠AED＝∠B ．
1. （1）求证：AD•AB＝AE•AC ．
2. （2）若AE＝EC＝2AD ，求 $\text{[math]}$ 的值．
3. （3）若AB＝6，AC＝4，求AD长的取值范围．
答案解析收藏纠错 + 选题
20. 已知点A（m₁ ， n₁），B（m₂ ， n₂）（m₁＜m₂）在一次函数y＝kx+b的图象上．
1. （1）用含有m₁ ， n₁ ， m₂ ， n₂的代数式表示k的值．
2. （2）若m₁+m₂＝3b ， n₁+n₂＝kb+4，b＞2．试比较n₁和n₂的大小，并说明理由．
答案解析收藏纠错 + 选题
21. (2023九上·杭州期末) 如图，在正五边形 $\text{[math]}$ 中，连结 $\text{[math]}$ 交 $\text{[math]}$ 于点F.
1. （1）求 $\text{[math]}$ 的度数.
2. （2）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
22. 数学实验
生活中，常常遇到需要测量物体长度、角度的情况，小聪同学思考：是否有既能测量长度，又能测量角度的多功能直尺？
小聪想自己做这样一把尺子：如图1，小聪准备了两条宽度为3cm的矩形纸带，并在点C处用可以转动的纽扣固定．小聪借助直角三角板的特殊度数，比较容易的找到表示 90°，60°，45°，30°角的刻度位置．那么另外的度数怎样标出呢？小聪开始思考原理：
1. （1）如图2，小聪将两条纸条叠合形成的四边形ABCD画出来，并分别作边DA ， BA的延长线AF ， AH ．小聪发现：①四边形ABCD是菱形；②∠FAH＝2∠ACD ．请证明这两个结论．
2. （2）小聪发现，在（1）的基础上，表示 90°，60°，45°，30°角的刻度位置可以用三角形的边角关系表示出来，当∠FAH＝90°时，∠ACD＝45°，则有CE＝AE＝3cm ，因此表示 90°角的位置就可以通过计算找到．请利用小聪的思路，算出表示 60°角的位置与点C的距离（精确到0.01）．（参考数据： $\text{[math]}$ ≈1.414， $\text{[math]}$ ≈1.732， $\text{[math]}$ ）．
3. （3）在以上思路启发下，小聪发现，在（1），（2）的基础上，对于任意位置的刻度的表示，只要完成三步任务：第一步，测量出直角△ACE 的直角边CE的长度m；第二步，计算出 $\text{[math]}$ 的值，这个值恰好是∠α 的正切值，即tanα＝ $\text{[math]}$ ；第三步，利用计算器算出α的值，并在尺子上标出刻度即可．做出的尺子如图3所示．
  请根据以上思路，计算出图2中CE的长度分别为4，2，1时，表示的角的刻度是多少（精确到分）．
  （参考数据：tan4°12'≈0.34，tan4°18'≈0.752，tan56°18'≈1.4994，tan56°24'≈1.5051，tan71°30'≈2.989，tan71°36'≈3.006）．
答案解析收藏纠错 + 选题
23. 某个农场有一个花卉大棚，是利用部分墙体建造的．其横截面顶部为抛物线型，大棚的一端固定在墙体OA上，另一端固定在墙体BC上，其横截面有2根支架DE ， FG ，相关数据如图1所示，其中支架DE＝BC ， OF＝DF＝BD ，这个大棚用了400根支架．
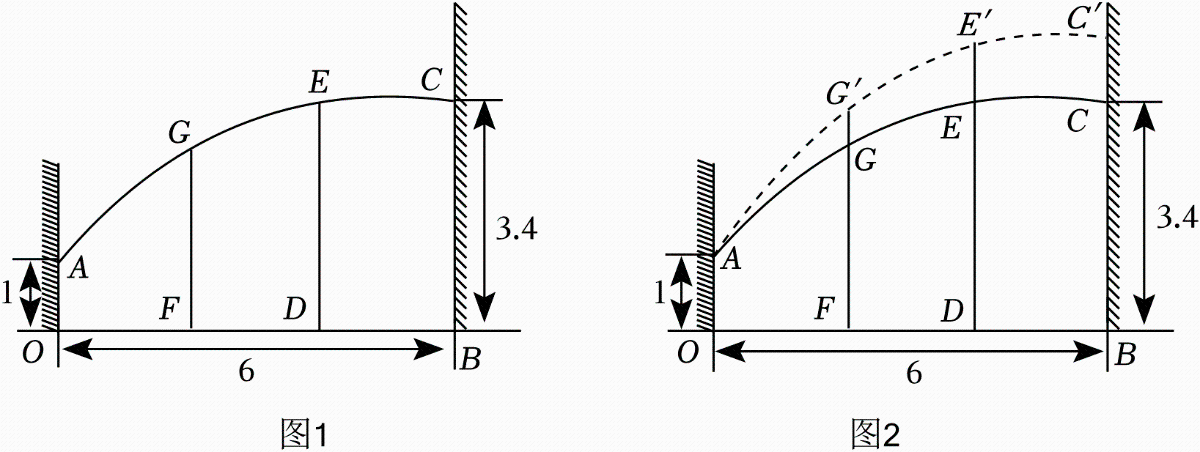
为增加棚内空间，农场决定将图1中棚顶向上调整，支架总数不变，对应支架的长度变化，如图2所示，调整后C与E上升相同的高度，增加的支架单价为60元/米（接口忽略不计），需要增加经费32000元．
1. （1）分别以OB和OA所在的直线为x轴和y轴建立平面直角坐标系．
  ①求出改造前的函数解析式．
  ②当CC^'＝1米，求GG^'的长度．
2. （2）只考虑经费情况下，求出CC^'的最大值．
答案解析收藏纠错 + 选题
24. 如图，在矩形ABCD中，点E ， F分别为对边AD ， BC的中点，线段EF交AC于点O ，延长CD于点G ，连结GE并延长交AC于点Q ，连结GF交AC于点P ，连结QF ．
1. （1）若DG＝ $\text{[math]}$ CD ．
  ①求证：点Q为OA的中点．
  ②若OA＝1，∠ACB＝30°，求QF的长．
2. （2）求证：FE平分∠QFP ．
3. （3）若CD＝mDG ，求 $\text{[math]}$ ．（结果用含m的代数式表示）.
答案解析收藏纠错 + 选题