2024年浙教版数学七（下）微素养核心突破1 平行线的判定与...

更新时间：2024-04-13 浏览次数：286 类型：复习试卷

一、选择题

1. (2024·长沙模拟) 光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图， $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七下·通榆月考) 传统文化风筝是由中国古代劳动人民发明于东周春秋时期的产物，其材质在不断改进之后，坊间开始用纸做风筝，称为“纸鸢”．如图所示的纸骨架中，与 $\text{[math]}$ 构成同旁内角的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八上·坪山期末) 太阳灶、卫星信号接收锅、探照灯及其他很多灯具都与抛物线有关．如图，从点 $\text{[math]}$ 照射到抛物线上的光线 $\text{[math]}$ ， $\text{[math]}$ 反射后沿着与 $\text{[math]}$ 平行的方向射出，已知图中 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八上·大余月考) 如图，一束平行于主光轴的光线经凸透镜折射后，其折射光线与一束经过光心 $\text{[math]}$ 的光线相交于点 $\text{[math]}$ ， $\text{[math]}$ 为焦点．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021七下·武义期中) 为增强学生体质，感受中国的传统文化，学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间，小聪把它抽象成图2的数学问题：已知AB∥CD，∠EAB＝80°， $\text{[math]}$ ，则∠E的度数是（）

A . 30° B . 40° C . 60° D . 70°

答案解析收藏纠错 + 选题
6. (2023·大安模拟) 如图，一束光线 $\text{[math]}$ 先后经平面镜 $\text{[math]}$ ， $\text{[math]}$ 反射后，反射光线 $\text{[math]}$ 与 $\text{[math]}$ 平行，当 $\text{[math]}$ 时， $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022七下·萝北期末) 平面镜反射光的规律是：射到中面镜上的光线和被反射的光线与平面镜所夹的锐角相等，即如图①中∠α＝∠β；若如图②光线m被平面镜a和b两次反射后，反射出的光线n和入射光线m平行，且∠1＝40°，则∠2等于（）

A . 40° B . 80° C . 90° D . 100°

答案解析收藏纠错 + 选题

二、填空题

8. (2024七下·南宁月考) 有经验的渔夫用鱼叉捕鱼时，不会将鱼叉对准他看到的鱼，这是由于光从空气射入水中时，发生折射现象.如图，水面 $\text{[math]}$ 与底面 $\text{[math]}$ 平行，光线 $\text{[math]}$ 从空气射入水中时发生了折射，变成光线 $\text{[math]}$ 射到水底 $\text{[math]}$ 处，射线 $\text{[math]}$ 是光线 $\text{[math]}$ 的延长线， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ .

答案解析收藏纠错 + 选题
9. (2023七下·孝义期末) 光从一种介质射向另一种介质时会发生折射．如图，用直线 $\text{[math]}$ ， $\text{[math]}$ 表示一块玻璃的两个面，且 $\text{[math]}$ ．现有一束光线 $\text{[math]}$ 从空气射向玻璃， $\text{[math]}$ 是折射光线， $\text{[math]}$ 为射线 $\text{[math]}$ 延长线上一点．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2023七上·哈尔滨期中) 如图1，当光线在空气进入水中时，会发生折射，满足入射角∠1与折射角∠2的度数比为4：3，如图2，在同一平面上，两条光线同时从空气进入水中，两条入射光线与水平面夹角度数分别为x ， y ，在水中两条折射光线的夹角度数为m、则m＝．（用含x ， y的式子表示）

答案解析收藏纠错 + 选题
11. 如图，平面反光镜AC斜放在地面AB上，一束光线从地面上的P点射出，DE是反射光线.已知∠APD=120°，若要使反射光线DE∥AB，则∠CAB应调节为°(提示：∠ADP=∠CDE，三角形的内角和等于180°).

答案解析收藏纠错 + 选题
12. (2023七下·石家庄期中) 如图1，将支架平面镜 $\text{[math]}$ 放置在水平桌面 $\text{[math]}$ 上，激光笔 $\text{[math]}$ 与水平天花板 $\text{[math]}$ 的夹角（ $\text{[math]}$ ）为 $\text{[math]}$ ，激光笔发出的入射光线 $\text{[math]}$ 射到 $\text{[math]}$ 上后，反射光线 $\text{[math]}$ 与 $\text{[math]}$ 形成 $\text{[math]}$ ，由光的反射定律可知， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的垂线 $\text{[math]}$ 所形成的夹角始终相等，即 $\text{[math]}$ ．
1. （1） $\text{[math]}$ 的度数为；
2. （2）如图2，点B固定不动，调节支架平面镜 $\text{[math]}$ ，调节角为 $\text{[math]}$ ．
  ①若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为；
  
  ②若反射光线 $\text{[math]}$ 恰好与 $\text{[math]}$ 平行，则 $\text{[math]}$ 的度数为．
答案解析收藏纠错 + 选题

三、作图题

13. (2020八上·镇海期中) 台球运动中，如果母球P击中桌边点A，经桌边反弹击中相邻的另一桌边，再次反弹，那么母球P经过的路线BC与PA平行吗？请你把台球母球P的完整路线P-A-B-C画出来，并作出适当的标注或说明.

答案解析收藏纠错 + 选题

四、解答题

14. (2023七下·前郭尔罗斯月考) 已知，MN ， EF分别表示两面互相平行的平面镜，即 $\text{[math]}$ ，一束光线AB照射到平面镜MN上，反射光线为BC ，此时 $\text{[math]}$ ；光线BC经平面镜EF反射后的反射光线为CD ，此时 $\text{[math]}$ .
求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2023七下·浏阳期末) 如图， $\text{[math]}$ ， $\text{[math]}$ 分别表示两个互相平行的镜面，一束光线 $\text{[math]}$ 照射到镜面 $\text{[math]}$ 上，反射光线为 $\text{[math]}$ ，此时 $\text{[math]}$ ；光线 $\text{[math]}$ 经过镜面 $\text{[math]}$ 反射后的光线为 $\text{[math]}$ ，此时 $\text{[math]}$ ．试判断 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由．
答： $\text{[math]}$ ．
理由：延长射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．
      $\text{[math]}$ ．
      $\text{[math]}$ $\text{[math]}$     ▲  （  ）
      $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ （已知）
      $\text{[math]}$ $\text{[math]}$     ▲  （等量代换）
又 $\text{[math]}$ $\text{[math]}$ ，
      $\text{[math]}$ $\text{[math]}$ （  ）
      $\text{[math]}$     ▲     （等量代换）
      $\text{[math]}$ $\text{[math]}$ （  ）

答案解析收藏纠错 + 选题
16. (2022七下·孝义月考) 潜望镜是指从海面下伸出海面或从低洼坑道伸出地面，用以窥探海面或地面上活动的装置．其构造与普通地上望远镜相同，另加两个反射镜使从摄入潜望镜的光线经两次反射而折向眼中．潜望镜常用于潜水艇、坑道和坦克内用以观察敌情．如图，进入潜望镜的光线和离开潜望镜的光线是平行的，光线经过镜子反射时，∠1＝∠2，∠3＝∠4，请猜想潜望镜中两面镜子的位置关系，并说明理由．

答案解析收藏纠错 + 选题
17. (2023七下·灵丘期中) 阅读下列材料，完成相应任务．
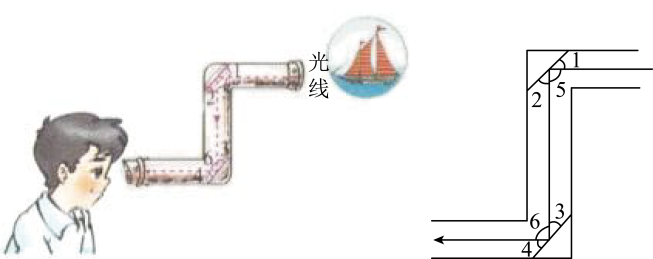
台球中的数学
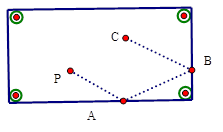
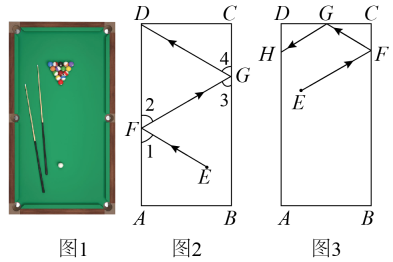
如图1是台球桌面实物图，图2是抽象出的数学图形，已知长方形桌面 $\text{[math]}$ 中， $\text{[math]}$ ，一个球在桌面上的点 $\text{[math]}$ 处滚向桌边 $\text{[math]}$ ，碰到 $\text{[math]}$ 上的点 $\text{[math]}$ 后反弹，再碰到 $\text{[math]}$ 边上的点 $\text{[math]}$ 后，再次反弹进入底袋点 $\text{[math]}$ ．在球碰到桌边反弹的过程中，击出线与桌边的夹角 $\text{[math]}$ 等于反弹线与桌边的夹角 $\text{[math]}$ ，同理 $\text{[math]}$ ．
1. （1）任务一：如图2，求证： $\text{[math]}$ ；
2. （2）任务二：如图3，若球在桌面的点 $\text{[math]}$ 处，经过两次反弹后碰到 $\text{[math]}$ 边上的点 $\text{[math]}$ 处，若 $\text{[math]}$ ，请你判断 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由．
答案解析收藏纠错 + 选题

五、实践探究题

18. (2023·广东模拟) 【学习新知】射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等．如图1，若入射光线与水平镜面夹角为 $\text{[math]}$ ，反射光线与水平镜面夹角为 $\text{[math]}$ ，则 $\text{[math]}$ ．
1. （1）【初步应用】如图2，有两块平面镜 $\text{[math]}$ ， $\text{[math]}$ ，入射光线 $\text{[math]}$ 经过两次反射，得到反射光线 $\text{[math]}$ ，若 $\text{[math]}$ ，证明： $\text{[math]}$ ；
2. （2）【拓展探究】如图3，有三块平面镜 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，入射光线 $\text{[math]}$ 经过三次反射，得到反射光线 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，若要使 $\text{[math]}$ ，则 $\text{[math]}$ 为多少度？
答案解析收藏纠错 + 选题

六、综合题

19. (2023七下·孝义期中) 阅读下列材料，并完成任务．
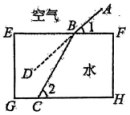
光线在不同介质中的传播速度是不同的，因此当光线从水中斜射向空气中时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中的折射光线也是平行的．如图，水面 $\text{[math]}$ 与杯底 $\text{[math]}$ 平行，光线 $\text{[math]}$ 与 $\text{[math]}$ 平行， $\text{[math]}$ 与 $\text{[math]}$ 平行．兴趣小组发现 $\text{[math]}$ ．证明过程如下：

证明：∵ $\text{[math]}$ ，
∴ $\text{[math]}$ （依据），
∵ $\text{[math]}$ ，
∴ $\text{[math]}$ ，
∴ $\text{[math]}$ ，
∴ $\text{[math]}$ ．
1. （1）任务一：上述材料中的“依据”指的是：；
2. （2）任务二：若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
20. (2023七下·贵州期中) 如图所示，把一根筷子一端放在水里，一端露出水面，筷子变弯了，它真的弯了吗？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变．
1. （1）请指出与∠1是同旁内角的有哪些角？请指出与∠2是内错角的有哪些角？
2. （2）若∠1＝115°，测得∠BOM＝145°，从水面上看斜插入水中的筷子，水下部分向上折弯了多少度？请说明理由．
答案解析收藏纠错 + 选题
21. (2022八上·九江期末) 实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b反射的光线为n．
1. （1）当 $\text{[math]}$ 时，若 $\text{[math]}$ ，则∠2＝，∠3＝；
2. （2）当 $\text{[math]}$ 时，若 $\text{[math]}$ ，则∠3＝；
3. （3）根据（1）（2）结果，反过来猜想：当两平面镜a，b的夹角∠3为多少度时， $\text{[math]}$ ．请说明理由（可以在图中添加适当的角度标记进行说明）
答案解析收藏纠错 + 选题
22. (2022七下·永年月考) 如图1展示了光线反射定律：EF是镜面AB的垂线，一束光线m射到平面镜AB上，被AB反射后的光线为n，则入射光线m，反射光线n与垂线EF所夹的锐角θ₁＝θ₂ ．
1. （1）在图1中，证明：∠1＝∠2．
2. （2）图2是潜望镜工作原理示意图，AB，CD是平行放置的两面平面镜．求证：m∥n．
答案解析收藏纠错 + 选题
23. (2021七下·洪山期中) 【学科融合】
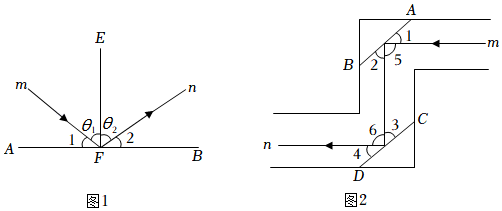
物理学中把经过入射点O并垂直于反射面的直线ON叫做法线，入射光线与法线的夹角i叫做入射角，反射光线与法线的夹角r叫做反射角（如图①）.由此可以归纳出如下的规律：

在反射现象中，反射光线、入射光线和法线都在同一平面内；反射光线、入射光线分别位于法线两侧；反射角等于入射角.这就是光的反射定律（rfectionlaw）.

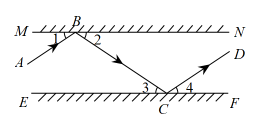
【数学推理】如图1，有两块平面镜OM，ON，且OM⊥ON，入射光线AB经过两次反射，得到反射光线CD.由以上光的反射定律，可知入射角与反射角相等，进而可以推得他们的余角也相等，即：∠1＝∠2，∠3＝∠4.在这样的条件下，求证：AB∥CD.

【尝试探究】两块平面镜OM，ON，且∠MON＝α，入射光线AB经过两次反射，得到反射光线CD.
1. （1）如图2，光线AB与CD相交于点E，则∠BEC＝；
2. （2）如图3，光线AB与CD所在的直线相交于点E，CBED＝β，则α与β之间满足的等量关系是.
答案解析收藏纠错 + 选题
24. (2023七下·瓯海期中) 光线反射是一种常见的物理现象，在生活中有广泛地应用.例如提词器可以帮助演讲者在看演讲词的同时也能面对摄像机，自行车尾部的反光镜等就是应用了光的反射原理.
1. （1）提词器的原理如图①，AB表示平面镜，CP表示入射光线，PD表示反射光线，∠CPD＝90°，求∠APC的度数；
2. （2）自行车尾部的反光镜在车灯照射下，能把光线按原来的方向返回（如图②），a表示入射光线，b表示反射光线，a∥b.平面镜AB与BC的夹角∠ABC＝ $\text{[math]}$ ，求 $\text{[math]}$ .
3. （3）如图③，若 $\text{[math]}$ ＝108°，设平面镜CD与BC的夹角∠BCD＝ $\text{[math]}$ （90°＜ $\text{[math]}$ ＜180°），入射光线a与平面镜AB的夹角为x（0°＜x＜90°），已知入射光线a从平面镜AB开始反射，经过2或3次反射，当反射光线b与入射光线a平行时，请直接写出 $\text{[math]}$ 的度数.（可用含x的代数式表示）.
答案解析收藏纠错 + 选题