四川省南充市2024年中考第一次诊断性考试数学模拟试题

更新时间：2024-04-28 浏览次数：33 类型：中考模拟

一、选择题(本大题共10个小题，每小题4分，共40分

1. (2024·南充模拟) 若2□(－2)＝0，则“□”中应填写的运算符号是（）

A . ＋ B . － C . × D . ÷

答案解析收藏纠错 + 选题
2. (2024·南充模拟) 如图，△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕点C顺时针旋转90°得对应△DEC ，连接BE ，则∠BED的大小为（）

A . 45° B . 30° C . 22.5° D . 15°

答案解析收藏纠错 + 选题
3. (2024·南充模拟) 甲、乙、丙、丁四名射击运动员进行射击测试，每人10次射击成绩的平均数 $\text{[math]}$ (单位：环)及方差 $\text{[math]}$ (单位： $\text{[math]}$ )如表所示，根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（）

甲
乙
丙
丁
$\text{[math]}$
9
9
9
8
$\text{[math]}$
6.5
2.4
1.6
0.3

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
4. (2024·南充模拟) 关于x的一元一次方程2x＋1－k＝0的解为1，则不等式组 $\text{[math]}$ 的整数解的个数是（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
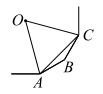
5. (2024·南充模拟) 如图，A ， B ， C是正多边形的顶点，O是正多边形的中心，若△AOC是等边三角形，则正多边形的边数为（）

A . 6 B . 9 C . 12 D . 15

答案解析收藏纠错 + 选题
6. (2024·南充模拟) 我国古代教育家墨子发现了小孔成像：用一个带有小孔的板遮挡在墙体与物之间，墙体上就会形成物的倒影，这种现象叫小孔成像。如图，根据小孔成像原理，已知蜡烛的火焰高AB＝2cm，当物距OE＝5cm，像距OF＝8cm时，火焰的像高CD为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·成都期中) 我国古代数学名著《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽”．大意是：“现请人代买一批椽，这批椽的总售价为6210文．如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽?”设6210文能买x株椽，则据题意可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
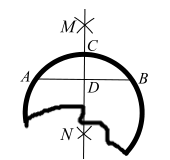
8. (2024·南充模拟) 要测量一个残损圆盘的半径．如图，小伟先在圆盘的圆弧上任取两点A ， B ，再分别以A ， B为圆心，大于 $\text{[math]}$ 长为半径画弧，两弧分别交于点M ， N ，过M ， N作直线，分别与弧AB ，弦AB交于点C ， D ．测得AB＝40cm，CD＝10cm，可计算出圆盘的半径为（）

A . 50cm B . 30cm C . 25cm D . 15cm

答案解析收藏纠错 + 选题
9. (2024九下·娄底期中) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
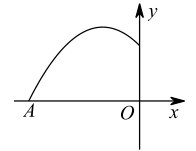
10. (2024·南充模拟) 如图，抛物线 $\text{[math]}$ 与x轴交于点A(－6，0)．点 $\text{[math]}$ ， $\text{[math]}$ 是抛物线上两点，当t≤x≤t＋3时，二次函数最大值记为 $\text{[math]}$ ，最小值记为 $\text{[math]}$ ，设 $\text{[math]}$ ，则m的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(本大题共6个小题，每小题4分，共24分)请将答案填在答题卡对应的横线上．

11. (2024·南充模拟) 计算： $\text{[math]}$ 的结果为．

答案解析收藏纠错 + 选题
12. (2024·南充模拟) 二维码是用某种特定的几何图形按一定规律在平面分布的黑白相间记录数据符号信息的图形，能在很小的面积内表达大量的信息．小强将二维码打印在纸片上(如图)，测得二维码的面积为 $\text{[math]}$ ，为了估计黑色阴影部分的面积，他在纸片二维码内随机掷点，经过大量实验，发现点落在黑色阴影的频率稳定在0.60左右，则据此估计二维码黑色阴影部分的面积约为．

答案解析收藏纠错 + 选题
13. (2024·南充模拟) 关于x的分式方程 $\text{[math]}$ 无解，则k的值为．

答案解析收藏纠错 + 选题
14. (2024·南充模拟) 如图，将矩形ABCD对折，使AB与CD边重合，得到折痕MN ，再将点A沿过点D的直线折叠到MN上，对应点为 $\text{[math]}$ ，折痕为DE ， AB＝10，BC＝6，则 $\text{[math]}$ 的长度为．

答案解析收藏纠错 + 选题
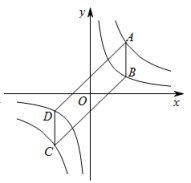
15. (2024·南充模拟) 如图，点A ， C在双曲线 $\text{[math]}$ 上，点B ， D在双曲线 $\text{[math]}$ 上， $\text{[math]}$ 轴，且四边形ABCD是平行四边形，则□ABCD的面积为．

答案解析收藏纠错 + 选题
16. (2024·南充模拟) 如图，点E是边长为8的正方形ABCD的边AD上一动点(端点A ， D除外)，以CE为边作正方形CEFG ， EF与AB交于点H ，连接BE ， BF ， BG ．下列四个结论：①BG＝DE；②∠FAB＝∠FEB；③当点E为AD中点时，H也是EF的中点；④当点E在AD边上运动时，AH有最大值为2．其中正确的结论是(填序号)．

答案解析收藏纠错 + 选题

三、解答题(本大题9个小题，共86分)解答应写出必要的文字说明、证明过程或演算步骤．

17. (2024·南充模拟) 计算：先化简，再求值： $\text{[math]}$ ，其中x＝－1．

答案解析收藏纠错 + 选题
18. (2024·南充模拟) 如图，在□ABCD中，点E是CD中点，连接AE并延长与BC的延长线交于点F ．
1. （1）求证：AD＝CF；
2. （2）连接AC ，若AB＝AF＝6，BC＝4，求□ABCD的面积．
答案解析收藏纠错 + 选题
19. (2024·南充模拟) 某初中学校为了解学生每周课外阅读时间，随机抽样调查了部分学生每周课外阅读时间，并根据调查结果，编制了如下两幅不完整的统计图表，根据图表信息，解答下列问题：
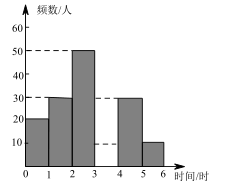
组别
时间(小时)
频数(人)
频率
A
0≤t<1
20
0.1
B
1≤t<2
30
0.15
C
2≤t<3
50
n
D
3≤t<4
m
0.3
E
4≤t<5
30
0.15
F
5≤t≤6
10
0.05
1. （1）填空：表中m＝人，n＝；
2. （2）若该校共有1500名学生，估计每周课外阅读时间不少于3小时的学生大约有多少人?
3. （3）该校计划从每周课外阅读时间在5小时及以上的学生中挑选出的2名男生和3名女生中随机选取2人参加知识竞赛，请用列表法或画树状图法，求恰好抽中性别相同的两名同学的概率．
答案解析收藏纠错 + 选题
20. (2024·南充模拟) 已知关于x的一元二次方程 $\text{[math]}$ 有两个实数根分别为 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求k的取值范围；
2. （2）若 $\text{[math]}$ ，求k的值．
答案解析收藏纠错 + 选题
21. (2024·南充模拟) 如图，一次函数y＝kx＋b(k≠0)与反比例函数 $\text{[math]}$ 的图象交于点A(－2，3)，B(6，n)，与x轴交于点.
1. （1）求一次函数和反比例函数的解析式；
2. （2）点P为x轴上一点，若△ABP的面积为10，求点P的坐标．
答案解析收藏纠错 + 选题
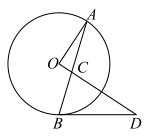
22. (2024·南充模拟) 如图，在⊙O中，AB是弦，过点O作OA⊥OC与AB交于点C ，在OC的延长线取点D ，使DC＝DB ．
1. （1）求证：BD是⊙O的切线；
2. （2）若BC＝4， $\text{[math]}$ ，求⊙O的半径长．
答案解析收藏纠错 + 选题
23. (2024·南充模拟) 电商小李在抖音平台上对一款成本单价为10元的商品进行直播销售，规定销售单价不低于成本价，且不高于成本价的3倍．通过前几天的销售发现，当销售定价为15元时，每天可售出700件，销售单价每上涨10元，每天销售量就减少200件，设此商品销售单价为x(元)，每天的销售量为y(件)．
1. （1）求y关于x之间的函数关系式，并写出x的取值范围；
2. （2）若销售该商品每天的利润为7500元，求该商品的销售单价；
3. （3）小李热心公益事业，决定每销售一件该商品就捐款m元(m>0)给希望工程，当每天销售最大利润为6000元时，求m的值．
答案解析收藏纠错 + 选题
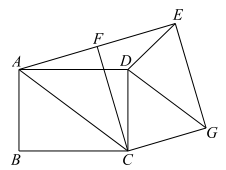
24. (2024·南充模拟) 如图，将矩形ABCD绕点C顺时针旋转，使点A，F，E三点共线，得到对应矩形EFCG，连接AF，AC，DG，DE．
1. （1）求证：AF＝CG；
2. （2）判断DG与AC的位置关系，并说明理由；
3. （3）若AB＝3，BC＝4，求tan∠AED的值．
答案解析收藏纠错 + 选题
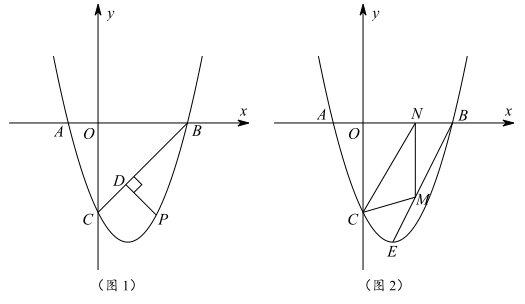
25. (2024·南充模拟) 如图，已知抛物线 $\text{[math]}$ 与x轴交于A(－1，0)，B两点，与y轴交于点C(0，－3)．
1. （1）求抛物线的解析式；
2. （2）如图1，点P是抛物线上位于第四象限内一动点，PD⊥BC于点D ，求PD的最大值及此时点P的坐标；
3. （3）如图2，点E是抛物线的顶点，点M是线段BE上的动点(点M不与B重合)，过点M作MN⊥x轴于N，是否存在点M，使△CMN为直角三角形?若存在，求出点M的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题