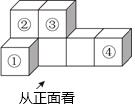

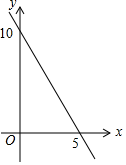 B .
B . 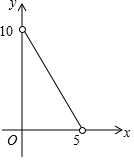 C .
C . 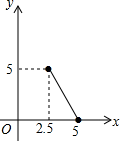 D .
D . 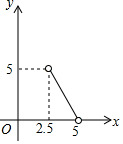


下面给出了部分信息:
抽取的七年级10名学生的竞赛成绩为:75,76,84,84,84,86,86,94,95,96;
抽取的八年级10名学生的竞赛成绩在B等级的为:81,83,84,88,88.
两个年级抽取的学生成绩的平均数、中位数、众数如下表所示:
学生 | 平均数 | 中位数 | 众数 |
七年级 | 86 | 85 | b |
八年级 | 86 | a | 88 |
抽取的八年级学生竞赛成绩扇形统计图:

根据以上信息,解答下列问题:

①与
满足一次函数关系,且第1天的日销售量为98件,第4天的日销售量为92件;
②与
函数关系如下图所示;

|
型号 |
原价 |
购买量少于30台 |
购买量不少于30台 |
|
A型 |
20万元/台 |
原价购买 |
打九折 |
|
B型 |
12万元/台 |
原价购买 |
打八折 |
①若要求这批机器人每小时一共能分拣垃圾20吨.设其中购买A型机器人x台(10≤x≤35),购买两种机器人总费用为W万元.求W与x的函数关系式,并说明如何购买总费用最少;
②为了加快垃圾分拣速度,垃圾处理厂计划用不超过140万元增购这两种机器人共10台,机器人公司全部以打折后价格销售,这10台机器人每小时最多处理多少吨垃圾?
(ⅰ)若 , 求点P的坐标,
(ⅱ)连接 ,
, 记
的面积为
,
的面积为
, 求
的最大值;