题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

湖南省长沙市岳麓区湖南师范大学附属滨江学校2023-2024...

更新时间：2024-06-27 浏览次数：9 类型：月考试卷

一、选择题（本题共10小题，每小题3分，共30分．）

1. (2024八下·岳麓月考) 要使得代数式 $\text{[math]}$ 有意义，则x的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·岳麓月考) 下列四组数据，能作为直角三角形的三边长的是（）

A . 2、4、6 B . 2、3、4 C . 5、7、12 D . 8、15、17

答案解析收藏纠错 + 选题
3. (2024八下·岳麓月考) 关于正比例函数 $\text{[math]}$ ，下列结论正确的是（）

A . 图象不经过原点 B . y随x的增大而增大 C . 图象经过第二、四象限 D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·岳麓月考) 如图，矩形 $\text{[math]}$ 的对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
5. (2024八下·岳麓月考) 如图，CD为Rt△ABC斜边AB上的中线，E为AC的中点．若AC＝8，CD＝5，则DE＝（　　）

A . 6 B . 5 C . 4 D . 3

答案解析收藏纠错 + 选题
6. (2024八下·岳麓月考) 如图，用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直，只需要用绳子分别测量比较书架的两条对角线AC，BD就可以判断，其推理依据是（）

A . 矩形的对角线相等 B . 矩形的四个角是直角 C . 对角线相等的四边形是矩形 D . 对角线相等的平行四边形是矩形

答案解析收藏纠错 + 选题
7. (2024八下·岳麓月考) 如图，在平行四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2024八下·岳麓月考) 已知林茂的家、体育场、文具店在同一直线上，图中的信息反映的过程是：林茂从家跑步去体育场，在体育场锻炼了一阵后又走到文具店买笔，然后再走回家，图中x表示时间，y表示林茂离家的距离，依据图中的信息，下列说法错误的是（）

A . 体育场离林茂家 $\text{[math]}$ B . 体育场离文具店 $\text{[math]}$ C . 林茂从体育场出发到文具店的平均速度是 $\text{[math]}$ D . 林茂出发 $\text{[math]}$ 时离家的距离是 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024八下·岳麓月考) 已知，如图，两张等宽的纸条交叉叠放在一起，重合部分构成四边形ABCD ，若测得A ， C之间的距离为 $\text{[math]}$ ， B ， D之间的距离为 $\text{[math]}$ ，则线段AB的长为（）

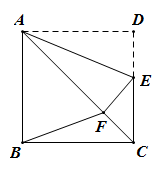
A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024八下·岳麓月考) 如图，在正方形ABCD中，E为CD边上一点，将△AED沿着AE翻折得到△AEF，点D的对应点F恰好落在对角线AC上，连接BF.若EF＝2，则BF²＝（）

A . 4 $\text{[math]}$ ＋4 B . 6＋4 $\text{[math]}$ C . 12 D . 8＋4 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本题共6小题，每小题3分，共18分）．

11. (2024八下·广东期末) 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 是正比例函数．

答案解析收藏纠错 + 选题
12. (2024九上·长沙开学考) 若 $\text{[math]}$ ，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
13. (2024八下·岳麓月考) 如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”（如图中的实线）．其实他们仅仅少走了m，却踩伤了花草．

答案解析收藏纠错 + 选题
14. 如图， $\text{[math]}$ 的顶点 $\text{[math]}$ 的坐标分别是 $\text{[math]}$ ．则顶点 $\text{[math]}$ 的坐标是．

答案解析收藏纠错 + 选题
15. (2024八下·岳麓月考) 如图，在正方形ABCD的外侧，作等边三角形ADE ， AC ， BE相交于点F ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
16. (2024八下·岳麓月考) 如图是一块农家菜地的平面图，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则这块菜地的面积为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题（本题共9小题，共72分．解答应写出文字说明，证明过程或演算步骤）

17. (2024九下·乐山模拟) 计算： $\text{[math]}$ ；

答案解析收藏纠错 + 选题
18. (2024九下·祁阳模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2024八下·岳麓月考) 已知正比例函数图象经过点 $\text{[math]}$ ．
1. （1）求这个函数的解析式；
2. （2）判断点 $\text{[math]}$ 是否在这个函数图象上；
3. （3）已知图象上两点 $\text{[math]}$ ， $\text{[math]}$ ，如果 $\text{[math]}$ ，比较 $\text{[math]}$ ， $\text{[math]}$ 的大小．
答案解析收藏纠错 + 选题
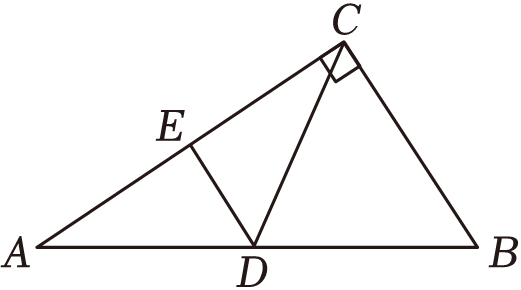
20. (2024八下·岳麓月考) 如图，在笔直的铁路上A ， B两点相距 $\text{[math]}$ ， C ， D为两村庄， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点A ， $\text{[math]}$ 于点B ，现要在AB上建一个中转站E ，使得C ， D两村到E站的距离相等．求E站应建在距AE点多远处？

答案解析收藏纠错 + 选题
21. (2024八下·岳麓月考) 小颖在实验操作课中发现：弹簧挂上物体后会伸长．已知一弹簧的长度（cm）与所挂物体的质量（kg）之间的关系如下表：
所挂物体的质量（kg）
0
1
2
3
4
5
弹簧的长度（cm）
11
12.5
14
15.5
17
18.5
1. （1）当没有挂物体时，弹簧的长度是cm．
2. （2）如果所挂物体的质量为 $\text{[math]}$ ，弹簧的长度为 $\text{[math]}$ ，根据上表写出y与x之间的关系式．
3. （3）当所挂物体的质量为 $\text{[math]}$ 时，求此时弹簧的长度．
4. （4）如果弹簧的最大伸长长度为 $\text{[math]}$ ，那么该弹簧最多能挂多重的物体？
答案解析收藏纠错 + 选题
22. (2024八下·岳麓月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ .
1. （1）求证：△ADE≌△FCE；
2. （2）若AB＝2BC，∠F＝36°.求∠B的度数.
答案解析收藏纠错 + 选题
23. (2024八下·岳麓月考) 某五金店用3000元购进A、B两种型号的机器零件1100个，购买A型零件与购买B型零件的费用相同．已知A型零件的单价是B型零件的1.2倍．
1. （1）求A、B两种型号零件的单价各是多少？
2. （2）若计划用不超过7000元的资金再次购买A、B两种型号的零件共2600个，已知两种零件的进价不变，则A型零件最多可购进多少个？
答案解析收藏纠错 + 选题
24. (2024八下·岳麓月考) 对于一个四边形给出如下定义：有一组对角相等且有一组邻边相等，则称这个四边形为奇特四边形．
1. （1）命题“另一组邻边也相等的奇特四边形为正方形”是（真或假）命题．
2. （2）如图，在正方形ABCD中，E是AB边上一点，F是AD延长线一点， $\text{[math]}$ ，连接EF ， EC ， FC ，取EF的中点G ，连接CG并延长交AD于点H ．探究：四边形BCGE是否是奇特四边形，如果是证明你的结论，如果不是请说明理由．
3. （3）在（2）的条件下，若四边形BCGE的面积为16，则 $\text{[math]}$ 的值是多少？
答案解析收藏纠错 + 选题
25. (2024八下·岳麓月考) 如图，平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ． F为矩形OABC对角线AC的中点，过点F的直线分别与OC、AB交于点D、E ．
1. （1）求证： $\text{[math]}$ ；
2. （2）设 $\text{[math]}$ ， $\text{[math]}$ 的面积为S ，求S与m的函数关系式；
3. （3）若点P在坐标轴上，平面内存在点Q ，使以P、Q、A、C为顶点的四边形是矩形，请直接写出点Q的坐标．
答案解析收藏纠错 + 选题

试卷信息