一、选择题(本大题共16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
-
-
-
4.
(2024·张家口模拟)
某中学积极响应党的号召,大力开展各项有益于德智体美劳全面发展的活动.子寒同学在某学期德智体美劳的评价得分如下图所示,则子寒同学五项评价的平均得分为( )

A . 7分
B . 8分
C . 9分
D . 10分
-
5.
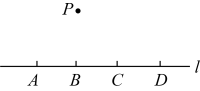
如图,点

,

,

,

均在直线

上,点

在直线

外,则经过其中任意三个点,最多可画出圆的个数为( )
A . 3个
B . 4个
C . 5个
D . 6个
-
-
A . 天翼的做法证明过程没有问题
B . 徍琛的做法证明过程没有问题
C . 天翼的做法添加的条件没有问题
D . 徍琛的做法添加的条件有问题
-
-
9.
(2024·张家口模拟)
在如图所示的网格中,若以点

为原点,

,

所在直线分别为

轴、

轴,则与点

在同一反比例函数

图像上的是( )

-
A . 该同学的做法只用了一次“三角形内角和定理”
B . 该结论只适用于锐角三角形
C . 若把“ 是
是 的角平分线
的角平分线 ,
,  的交点”替换为“
的交点”替换为“ 是
是 的外心”,该结论不变
D . 若把“
的外心”,该结论不变
D . 若把“ 是
是 的角平分线
的角平分线 ,
,  的交点”替换为“
的交点”替换为“ 是
是 的内心”,该结论不变
的内心”,该结论不变
-
11.
(2024·张家口模拟)
如图,传送带的一个转动轮的半径为

, 转动轮转

, 传送带上的物品

被传送

, 则

为( )

A . 90
B . 108
C . 120
D . 无法判断
-
12.
(2024·张家口模拟)
如图是一款抛物线型落地灯示意图,防滑螺母

为抛物线支架的最高点,灯罩

距离地面1.5米,最高点

距灯柱

的水平距离为1.6米,灯柱

米,若茶几摆放在灯罩的正下方,则茶几正下方位置到灯柱的距离

为( )

A . 3.2米
B . 0.32米
C . 2.5米
D . 1.6米
-
13.
(2024·张家口模拟)
如图,点

,

是边

的三等分点,

的面积为27,现从

边上取一点

, 过点

沿平行

的方向剪下一个面积为10的三角形,则点

在( )

A . 线段 上
B . 线段
上
B . 线段 上,且靠近点
上,且靠近点 C . 线段
C . 线段 上,且靠近点
上,且靠近点 D . 线段
D . 线段 上
上
-
14.
(2024·张家口模拟)
如图,将

的

按下面的方式放置在一把刻度尺上:顶点

与尺下沿的左端点重合,

与尺下沿重合,

与尺上沿的交点

在尺上的读数为

.若按相同的方式将

的

放置在该刻度尺上,则

与尺上沿的交点

在尺上的读数是(结果精确到

, 参考数据

,

,

).( )

-
15.
(2024·张家口模拟)
如图是

,

, …,

十个点在圆上的位置图,且此十点将圆周分成十等份.连接

和

, 并延长交于一点,连接

和

并延长交于一点,则夹角各是多少( )

-
A . 当 时,函数
时,函数 的最小值为
的最小值为 B . 当
B . 当 时,函数
时,函数 的最小值为
的最小值为 C . 当
C . 当 时,函数
时,函数 的最小值为
的最小值为 D . 当
D . 当 时,函数
时,函数 的最小值为
的最小值为
二、填空题(本大题有3个小题,共10分.17和18题各3分,19小题有2个空,每空2分)
-
-
18.
(2024·张家口模拟)
如图,正六边形

的边长为1,分别以其对角线

,

为边作正方形,则两个阴影部分的面积差

的值为

-
19.
(2024·张家口模拟)
如图①是小明制作的一副弓箭,

,

分别是弓臂

与弓弦

的中点,弓弦

, 沿

方向拉弓的过程中,假设弓臂

始终保持圆弧形,弓弦长度不变.如图②,当弓箭从自然状态的点

拉到点

时,有

,

.

⑴图②中,弓臂两端 ,
,  之间的距离是
之间的距离是 ;
;
⑵如图③,将弓箭继续拉到点 , 使弓臂
, 使弓臂 为半圆,则
为半圆,则 的值为
的值为
三、解答题(本大题共7个小题,共68分.解答应写出文字说明、证明过程或演算步骤)
-
-
21.
(2024·张家口模拟)
如图,张老师想用长为

的栅栏,再借助房屋的外墙直线

(外墙足够长)围成一个矩形车棚

, 并在边

上留一个

宽的门(建在

处,另用其他材料).

-
(1)
当车棚的长和宽分别为多少米时,能围成一个面积为

的车棚;
-
(2)
车棚的面积能达到

吗?如果能,请你给出设计方案;如果不能,请说明理由.
-
22.
(2024·张家口模拟)
2023年春节期间调研小组随机调查了某新开放景区的部分参观群众,为本景区打分(打分按从高到低分为5个分值:5分,4分,3分,2分,1分),并将调查结果绘制成不完整的条形统计图(如图①)和扇形统计图(如图②).根据以上信息,回答下列问题:

-
(1)
本次共调查了 ▲ 名参观群众,并补全条形统计图,分值的众数是,中位数是 ▲ ;
-
(2)
为了进一步研究,调研小组又增加调查了5位参观者,若他们的打分分别为:5,4,4,5,3,则增加调查人数前后,本次活动打分分值的中位数与原来是否相同?并简要说明理由;
-
(3)
若从打分较低的四人中随机抽取2名做情况反馈,发现抽取的2人恰为一个成人一个儿童的概率为

, 直接写出这4人中成人与儿童的可能分布情况.
-
23.
(2024·张家口模拟)
如图,点

在数轴上对应的数是-2,以原点

为圆心,

的长为半径作优弧

, 使点

在原点的左上方,且

, 点

为

的中点,点

在数轴上对应的数为4.

-
(1)
求扇形

的面积;
-
-
-
-
(2)
若

, 求点

的坐标;
-
(3)
连接

, 记

的面积为

, 若

, 求

的取值范围.
-
25.
(2024·张家口模拟)
如图,在

中,

,

,

.动点

以每秒2个单位的速度从点

出发,沿着

的方向运动,当点

到达点

时,运动停止.点

是点

关于点

的对称点,过点

作

于点

, 以

,

为邻边作平行四边形

, 设点

的运动时间为

秒.

-
(1)
求

的长;
-
(2)
当

时,求证:

;
-
(3)
是否存在这样的

值,使得平行四边形

为菱形?若存在,请求出

值;若不存在,请说明理由.
-
26.
(2024·张家口模拟)
某课外小组利用几何画板来研究二次函数的图象,给出二次函数解析式

, 通过输入不同的

,

的值,在几何画板的展示区内得到对应的图象.

-
(1)
若输入

,

, 得到如图①所示的图象,求顶点

的坐标及抛物线与

轴的交点

,

的坐标
-
 D .
D . 





,
之间的距离是
;
, 使弓臂
为半圆,则
的值为


,
的值后,得到如图②的图象恰好经过
,
两点,求出
,
的值;
, 嘉嘉输入
, 若得到二次函数的图象与线段
有公共点,求淇淇输入
的取值范围.