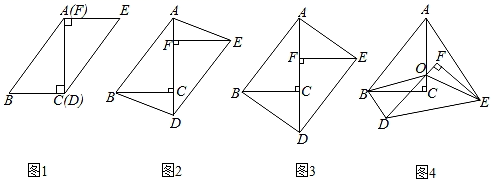
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
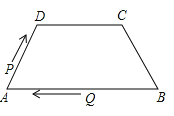




①求证:;
②求证:;

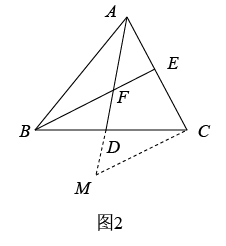


小明发现可以类比以上思路进行证明.
证明:如图2,延长AD至点M,使MD=FD,连接MC,……
请你根据小明的思路完成证明过程.
①请你判断线段EF和AE的数量关系是 ▲ , 并说明理由;
②若菱形ABCD的边长为6,CF=CE,请直接写出CF的长.
在平面内,已知线段 ,
, 则线段
的最小值为.
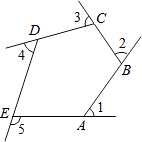
如图1,在平行四边形中,
,
,
, P是边
的中点,Q是边
上一动点,将三角形
沿
所在直线翻折,得到三角形
, 连接
, 求
的最小值.
如图2,平行四边形为某公园平面示意图,扇形
为该公园的人口广场,已知
,
,
,
. 为了提升游客体验感,工作人员准备在弧
上找一点P , 沿
,
修两条绿色通道,并在
上方和
右方区域种植花卉供游客观赏,其余地方修建其他设施,求其他设施区域
面积的最小值.