四川省宜宾市2024届高三下学期高考适应性考试（三模）文科数...

更新时间：2024-06-06 浏览次数：15 类型：高考模拟

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合要求．

1. (2024高三下·宜宾模拟) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高三下·宜宾模拟) 已知复数z满足 $\text{[math]}$ 且 $\text{[math]}$ 是z的共轭复数，则 $\text{[math]}$ （）

A . ―1 B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高一下·安居月考) 已知一组数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数是2，方差是3，则对于以下数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 下列选项正确的是（）

A . 平均数是4，方差是6 B . 平均数是4，方差是7 C . 平均数是5，方差是7 D . 平均数是5，方差是12

答案解析收藏纠错 + 选题
4. (2024高三下·宜宾模拟) 若曲线 $\text{[math]}$ 的一条切线方程是 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . ―2 B . 1 C . ―1 D . e

答案解析收藏纠错 + 选题
5. (2024高三下·宜宾模拟) 明朝数学家程大位著的《算法统宗》里有一道著名的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大、小和尚各几丁？”如图所示的程序框图反映了此题的一个算法，执行图中的程序框图，则输出n＝（）

A . 72 B . 75 C . 78 D . 80

答案解析收藏纠错 + 选题
6. (2024高三下·宜宾模拟) 下列各式中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高三下·宜宾模拟) 某零售行业为了解宣传对销售额的影响，在本市内随机抽取了5个大型零售卖场，得到其宣传费用x（单位：万元）和销售额y（单位：万元）的数据如下：
x（万元）
3
4
5
6
7
y（万元）
45
50
60
65
70
由统计数据知y与x满足线性回归方程 $\text{[math]}$ ，其中 $\text{[math]}$ ，当宣传费用 $\text{[math]}$ 时，销售额y的估计值为（）

A . 89.5 B . 90.5 C . 92.5 D . 94.5

答案解析收藏纠错 + 选题
8. (2024高三下·宜宾模拟) 已知函数 $\text{[math]}$ 在 $\text{[math]}$ 上单调递减且对任意 $\text{[math]}$ 满足 $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024高三下·宜宾模拟) 在直三棱柱 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点P在四边形 $\text{[math]}$ 内（含边界）运动，当 $\text{[math]}$ 时，点P的轨迹长度为 $\text{[math]}$ ，则该三棱柱的表面积为（）

A . 4 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高三下·宜宾模拟) 已知抛物线C： $\text{[math]}$ ，过动点P作两条相互垂直的直线，分别与抛物线C相切，则点P的轨迹是（）

A . 一条抛物线 B . 一个圆 C . 一条直线 D . 一段线段

答案解析收藏纠错 + 选题
11. (2024高三下·宜宾模拟) 定义在 $\text{[math]}$ 上的单调函数 $\text{[math]}$ ，对任意的 $\text{[math]}$ 都有 $\text{[math]}$ ，若方程 $\text{[math]}$ 有两个不同的实数根，则实数m的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024高三下·宜宾模拟) 已知E ， F分别是棱长为2的正四面体ABCD的对棱AD ， BC的中点.过EF的平面 $\text{[math]}$ 与正四面体ABCD相截，得到一个截面多边形 $\text{[math]}$ ，则下列说法正确的是（）

A . 截面多边形 $\text{[math]}$ 不可能是平行四边形 B . 截面多边形 $\text{[math]}$ 的周长是定值 C . 截面多边形 $\text{[math]}$ 的周长的最小值是 $\text{[math]}$ D . 截面多边形 $\text{[math]}$ 的面积的取值范围是 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：本大题共4个小题，每小题5分，共20分．

13. (2024高三下·宜宾模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为.

答案解析收藏纠错 + 选题
14. (2024高三下·宜宾模拟) 已知数列 $\text{[math]}$ 是公差不为0的等差数列， $\text{[math]}$ ，且满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等比数列，则数列 $\text{[math]}$ 前6项的和．

答案解析收藏纠错 + 选题
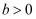
15. (2024高三下·宜宾模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ 为双曲线C： $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的左、右焦点，P为双曲线右支上任意一点，点Q的坐标为 $\text{[math]}$ ．若 $\text{[math]}$ 有最大值，则双曲线C的离心率的取值范围是．

答案解析收藏纠错 + 选题
16. (2024高三下·宜宾模拟) 已知点O ， A ， B ， C均在同一平面内， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 取最大值时，BC＝．

答案解析收藏纠错 + 选题

三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必做题：共60分．

17. (2024高三下·宜宾模拟) 某地为调查年龄在35―50岁段人群每周的运动情况，从年龄在35―50岁段人群中随机抽取了200人的信息，将调查结果整理如下：

女性
男性
每周运动超过2小时
60
80
每周运动不超过2小时
40
20
参考公式： $\text{[math]}$ ， $\text{[math]}$ ．
$\text{[math]}$
0.10
0.05
0.025
0.010
0.001
$\text{[math]}$
2.706
3.841
5.024
6.635
10.828
1. （1）根据以上信息，能否有99%把握认为该地年龄在35―50岁段人群每周运动超过2小时与性别有关？
2. （2）在以上被抽取且每周运动不超过2小时的人中，按性别进行分层抽样，共抽6人．再从这6人中随机抽取2人进行访谈，求这2人中至少有1人是女性的概率．
答案解析收藏纠错 + 选题
18. (2024高三下·宜宾模拟) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ，（ $\text{[math]}$ ）．
1. （1）证明：数列 $\text{[math]}$ 是等比数列，并求出数列 $\text{[math]}$ 的通项公式；
2. （2）设 $\text{[math]}$ ，数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ，若 $\text{[math]}$ 对于任意 $\text{[math]}$ 恒成立，求实数m的取值范围．
答案解析收藏纠错 + 选题
19. (2024高三下·宜宾模拟) 如图，在四棱锥 $\text{[math]}$ 中，底面ABCD是正方形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点E为线段PC的中点，点F在线段AB上，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）求三棱锥 $\text{[math]}$ 的体积．
答案解析收藏纠错 + 选题
20. (2024高三下·宜宾模拟) 已知函数 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，求函数 $\text{[math]}$ 过原点的切线方程；
2. （2）若 $\text{[math]}$ 有三个零点，求a的取值范围．
答案解析收藏纠错 + 选题
21. (2024高三下·宜宾模拟) 已知椭圆E： $\text{[math]}$ 的左右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，过焦点 $\text{[math]}$ 斜率为 $\text{[math]}$ 的直线 $\text{[math]}$ 与椭圆E交于A ， B两点，过焦点 $\text{[math]}$ 斜率为 $\text{[math]}$ 的直线 $\text{[math]}$ 与椭圆E交于C ， D两点，且 $\text{[math]}$ ．
1. （1）求直线 $\text{[math]}$ 与 $\text{[math]}$ 的交点N的轨迹M的方程；
2. （2）若直线OA ， OB ， OC ， OD的斜率分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，问在（1）的轨迹M上是否存在点P ，满足 $\text{[math]}$ ，若存在，求出点P坐标；若不存在，说明理由．
答案解析收藏纠错 + 选题

四、（二）选做题：共10分．请考生在第22、23题中选一题作答．如果多做，则按所做的第一题计分．

22. (2024高三下·宜宾模拟) ［选修4-4：坐标系与参数方程］
在平面直角坐标系中，过点 $\text{[math]}$ 的直线l的参数方程为 $\text{[math]}$ （t为参数）．以原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为 $\text{[math]}$ （ $\text{[math]}$ ）．直线l与曲线C相交于M ， N两点．
1. （1）求直线l的普通方程及曲线C的直角坐标方程；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等比数列，求实数a的值．
答案解析收藏纠错 + 选题
23. (2024高三下·宜宾模拟) ［选修4-5：不等式选讲］
已知函数 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的最小值；
2. （2）若 $\text{[math]}$ 恒成立，求实数a的取值范围．
答案解析收藏纠错 + 选题