四川省宜宾市2024届高三下学期高考适应性考试（三模）理科数...

更新时间：2024-05-27 浏览次数：22 类型：高考模拟

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合要求．

1. (2024高三下·宜宾模拟) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 0 B . 0或-2 C . 0或2 D . 2或-2

答案解析收藏纠错 + 选题
2. (2024高三下·宜宾模拟) 为了加深师生对党史的了解，激发广大师生知史爱党、知史爱国的热情，某校举办了“学党史、育新人”的党史知识竞赛，并将1000名师生的竞赛成绩（满分100分，成绩取整数）整理成如图所示的频率分布直方图，则下列说法错误的是（）

A . a的值为0.005 B . 估计这组数据的众数为75分 C . 估计成绩低于60分的有250人 D . 估计这组数据的中位数为 $\text{[math]}$ 分

答案解析收藏纠错 + 选题
3. (2024高三下·宜宾模拟) 下列各式中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高三下·宜宾模拟) 已知虚数z满足 $\text{[math]}$ ，且 $\text{[math]}$ 是z的共轭复数，则下列结论错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高三下·宜宾模拟) 若曲线 $\text{[math]}$ 在 $\text{[math]}$ 处的切线也是曲线 $\text{[math]}$ 的切线，则 $\text{[math]}$ （）

A . -2 B . 1 C . -1 D . e

答案解析收藏纠错 + 选题
6. (2024高三下·宜宾模拟) 在 $\text{[math]}$ 的展开式中，含x项的系数是（）

A . ―180 B . ―90 C . 90 D . 180

答案解析收藏纠错 + 选题
7. (2024高三下·宜宾模拟) 若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高三下·宜宾模拟) 已知正四棱锥 $\text{[math]}$ 的所有棱长均为4，E为棱PA的中点，则异面直线BE与PC所成角的余弦值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024高三下·宜宾模拟) 某学校开展“五育并举”的选修课，其中体育开设了6门课，分别为篮球、足球、排球、网球、羽毛球、乒乓球，甲、乙两名学生准备从中各选择2门课学习，则甲、乙选修的课中至少有1门相同的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高三下·宜宾模拟) 已知抛物线C： $\text{[math]}$ ，过动点P作两条相互垂直的直线，分别与抛物线C相切于点A ， B ，则 $\text{[math]}$ 面积的最小值是（）

A . 6 B . 9 C . 12 D . 18

答案解析收藏纠错 + 选题
11. (2024高三下·宜宾模拟) 定义在 $\text{[math]}$ 上的单调函数 $\text{[math]}$ ，对任意的 $\text{[math]}$ 有 $\text{[math]}$ 恒成立，若方程 $\text{[math]}$ 有两个不同的实数根，则实数m的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024高三下·宜宾模拟) 已知E ， F分别是棱长为2的正四面体ABCD的对棱AD ， BC的中点.过EF的平面 $\text{[math]}$ 与正四面体ABCD相截，得到一个截面多边形 $\text{[math]}$ ，则正确的选项是（）
①截面多边形 $\text{[math]}$ 可能是三角形或四边形．
②截面多边形 $\text{[math]}$ 周长的取值范围是 $\text{[math]}$ ．
③截面多边形 $\text{[math]}$ 面积的取值范围是 $\text{[math]}$ ．
④当截面多边形 $\text{[math]}$ 是一个面积为 $\text{[math]}$ 的四边形时，四边形的对角线互相垂直．

A . ①③ B . ②④ C . ①②③ D . ①③④

答案解析收藏纠错 + 选题

二、填空题：本大题共4个小题，每小题5分，共20分．

13. (2024高三下·宜宾模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
14. (2025·) 已知数列 $\text{[math]}$ 是公差不为0的等差数列， $\text{[math]}$ ，且满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等比数列，则数列 $\text{[math]}$ 前6项的和为．

答案解析收藏纠错 + 选题
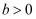
15. (2024高三下·宜宾模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ 为双曲线C： $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的左、右焦点，P为双曲线右支上任意一点，点Q的坐标为 $\text{[math]}$ ．若 $\text{[math]}$ 有最大值，则双曲线C的离心率的取值范围是．

答案解析收藏纠错 + 选题
16. (2024高三下·宜宾模拟) 已知点O ， A ， B在同一平面内且A为定点， $\text{[math]}$ ， $\text{[math]}$ ， C ， D分别是点B轨迹上的点且 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值与最小值之和是．

答案解析收藏纠错 + 选题

三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必做题：共60分．

17. (2024高三下·宜宾模拟) 某地为调查年龄在35―50岁段人群每周的运动情况，从年龄在35―50岁段人群中随机抽取了200人的信息，将调查结果整理如下：

女性
男性
每周运动超过2小时
60
80
每周运动不超过2小时
40
20
参考公式： $\text{[math]}$ ， $\text{[math]}$ ．
$\text{[math]}$
0.10
0.05
0.025
0.010
0.001
$\text{[math]}$
2.706
3.841
5.024
6.635
10.828
1. （1）根据以上信息，能否有99%把握认为该地年龄在35―50岁段人群每周运动超过2小时与性别有关？
2. （2）用样本估计总体，从该地年龄在35―50岁段人群中随机抽取3人，设抽取的3人中每周运动不超过2小时的人数为X ，求X的分布列和数学期望 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024高三下·宜宾模拟) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ，（ $\text{[math]}$ ）．
1. （1）证明：数列 $\text{[math]}$ 是等比数列，并求出数列 $\text{[math]}$ 的通项公式；
2. （2）设 $\text{[math]}$ ，数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ，若 $\text{[math]}$ 对于任意 $\text{[math]}$ 恒成立，求实数m的取值范围．
答案解析收藏纠错 + 选题
19. (2024高三下·宜宾模拟) 如图，在四棱锥 $\text{[math]}$ 中，底面ABCD是正方形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点E为线段PC的中点，点F在线段AB上．
1. （1）若 $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）若F是AB上靠近点B的三等分点，求平面DEF与平面DPA所成的锐二面角的余弦值．
答案解析收藏纠错 + 选题
20. (2024高三下·宜宾模拟) 已知椭圆E： $\text{[math]}$ 的左右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ， P是直线l： $\text{[math]}$ 上不同于原点O的一个动点，斜率为 $\text{[math]}$ 的直线 $\text{[math]}$ 与椭圆E交于A ， B两点，斜率为 $\text{[math]}$ 的直线 $\text{[math]}$ 与椭圆E交于C ， D两点．
1. （1）求 $\text{[math]}$ 的值；
2. （2）是否存在点P ，满足 $\text{[math]}$ ？若存在，求出点P的坐标；若不存在，说明理由．（ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别为直线OA ， OB ， OC ， OD的斜率）
答案解析收藏纠错 + 选题
21. (2024高三下·宜宾模拟) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 过原点的切线方程；
2. （2）求证：存在 $\text{[math]}$ ，使得 $\text{[math]}$ 在区间 $\text{[math]}$ 内恒成立，且 $\text{[math]}$ 在 $\text{[math]}$ 内有解．
答案解析收藏纠错 + 选题

四、（二）选做题：共10分．请考生在第22、23题中选一题作答．如果多做，则按所做的第一题计分．

22. (2024高三下·宜宾模拟) ［选修4-4：坐标系与参数方程］
在平面直角坐标系中，过点 $\text{[math]}$ 的直线l的参数方程为 $\text{[math]}$ （t为参数）．以原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为 $\text{[math]}$ （ $\text{[math]}$ ）．直线l与曲线C相交于M ， N两点．
1. （1）求直线l的普通方程及曲线C的直角坐标方程；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等比数列，求实数a的值．
答案解析收藏纠错 + 选题
23. (2024高三下·宜宾模拟) ［选修4-5：不等式选讲］
已知函数 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的最小值；
2. （2）若 $\text{[math]}$ 恒成立，求实数a的取值范围．
答案解析收藏纠错 + 选题