（通用版）2024年中考数学重点知识冲刺训练---统计与概率

更新时间：2024-05-20 浏览次数：21 类型：三轮冲刺

一、选择题

1. (2024九下·哈尔滨模拟) 在一个不透明的袋子里装有2个红球和5个白球，它们除颜色外都相同，从中任意摸出1个球，则摸出的球为红球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 空气的成分（除去水汽、杂质等）是：氮气约占78%，氧气约占21%，其他微量气体约占1%.要反映上述信息，宜采用的统计图是（）

A . 条形统计图 B . 折线统计图 C . 扇形统计图 D . 频数直方图

答案解析收藏纠错 + 选题
3. 上周双休日，某班8名同学课外阅读的时间如下（单位：时）：1，4，2，4，3，3，4，5.这组数据的众数是（）

A . 1时 B . 2时 C . 3时 D . 4时

答案解析收藏纠错 + 选题
4. 祖冲之是中国数学史上伟大的数学家，他把圆周率精确到小数点后7位，这是祖冲之最重要的数学贡献.数学活动课上，同学们对圆周率的小数点后100位数字进行了统计：
数字
0
1
2
3
4
5
6
7
8
9
频数
8
8
12
11
10
8
9
8
12
14
那么，圆周率的小数点后100位数字的众数与中位数分别为（）

A . 9，5 B . 14，4.5 C . 14，5 D . 9，4.5

答案解析收藏纠错 + 选题
5. (2024六下·博山期末) 下列调查中，适宜采用全面调查方式的是（）

A . 了解某种灯泡的使用寿命 B . 了解一批冷饮的质量是否合格 C . 了解全国八年级学生的视力情况 D . 了解某班同学中哪个月份出生的人数最多

答案解析收藏纠错 + 选题
6. (2024·从江模拟) 在某次数学测试中，10名学生的测试成绩（单位：分）统计如图所示，则这10名学生的测试成绩的众数是（）.

A . 87.5 B . 90 C . 95 D . 92.5

答案解析收藏纠错 + 选题
7. (2024·明水模拟) 为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求，学校要求学生每天坚持体育锻炼．小亮记录了自己一周内每天校外锻炼的时间（单位：分钟），并制作了如图所示的统计图．

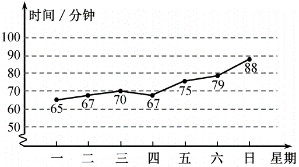
根据统计图，下列关于小亮该周每天校外锻炼时间的描述，正确的是（）

A . 平均数为70分钟 B . 众数为67分钟 C . 中位数为67分钟 D . 方差为0

答案解析收藏纠错 + 选题
8. 为落实教育部办公厅、中共中央宣传部办公厅关于《第41批向全国中小学生推荐优秀影片片目》的通知精神，某校七、八年级分别从如图所示的三部影片中随机选择一部组织本年级学生观看，则这两个年级选择的影片相同的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 为检测学生体育锻炼效果，从某班随机抽取10名学生进行篮球定时定点投篮检测，投篮进球数统计如图所示．对于这10名学生的定时定点投篮进球数，下列说法中错误的是（）

A . 中位数是5 B . 众数是5 C . 平均数是5.2 D . 方差是2

答案解析收藏纠错 + 选题
10. (2017·桥西模拟) 小华进行了5次射击训练后，计算出这5次射击的平均成绩为8环，方差为s₁² ，随后小华又进行了第6次射击，成绩恰好是8环，并计算出这6次射击成绩的方差为s₂² ，则下列说法正确的是（）

A . s₁²=s₂² B . s₁²＜s₂² C . s₁²＞s₂² D . 无法确定s₁²与s₂²的大小

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·中江模拟) 一个仅装有球的不透明布袋里只有6个红球和 $\text{[math]}$ 个白球（仅有颜色不同）．若从中任意摸出一个球是红球的概率为 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024九下·郁南模拟) 下表为某中学统计的七年级500名学生体重达标情况（单位：人），在该年级随机抽取一名学生，该生体重“标准”的概率是.

“偏瘦”

“标准”

“超重”

“肥胖”

80

350

46

24

答案解析收藏纠错 + 选题
13. (2024九下·南山模拟) 端午节早上，小颖为全家人蒸了2个蛋黄粽，3个鲜肉粽，她从中随机挑选了两个孝敬爷爷奶奶，请问爷爷奶奶吃到同类粽子的概率是．

答案解析收藏纠错 + 选题
14. (2022·新都模拟) 将一副三角板中的两个三角板的两条直角边重合叠放在一起，三角板 $\text{[math]}$ 固定不动，三角板 $\text{[math]}$ 绕直角顶点O按顺时针或逆时针方向任意转动一个角 $\text{[math]}$ ，如图所示，当这两块三角板各有一条边互相垂直时，在 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 这七个度数中是 $\text{[math]}$ 的度数的概率为.

答案解析收藏纠错 + 选题

三、解答题

15. (2020九上·晋州期中) 体育课上，老师为了解女学生定点投篮的情况，随机抽取8名女生进行每人4次定点投篮的测试，进球数的统计如图所示．
1. （1）求女生进球数的平均数、中位数；
2. （2）投球4次，进球3个以上（含3个）为优秀，全校有女生1200人，估计为“优秀”等级的女生约为多少人？
答案解析收藏纠错 + 选题
16. (2017·湖州)
为积极创建全国文明城市，某市对某路口的行人交通违章情况进行了 $\text{[math]}$ 天的调查，将所得数据绘制成如下统计图（图2不完整）：
请根据所给信息，解答下列问题：
1. （1）第 $\text{[math]}$ 天，这一路口的行人交通违章次数是多少次？这 $\text{[math]}$ 天中，行人交通违章 $\text{[math]}$ 次的有多少天？
2. （2）请把图2中的频数直方图补充完整；
3. （3）通过宣传教育后，行人的交通违章次数明显减少．经对这一路口的再次调查发现，平均每天的行人交通违章次数比第一次调查时减少了 $\text{[math]}$ 次，求通过宣传教育后，这一路口平均每天还出现多少次行人的交通违章？
答案解析收藏纠错 + 选题
17. 在一次数学文化课题活动中，把一副数学文化创意扑克牌中的4张扑克牌（如图所示）洗匀后正面向下放在桌面上，从中随机抽取2张牌，请你用列表或画树状图的方法，求抽取的2张牌的数字之和为偶数的概率．

答案解析收藏纠错 + 选题
18. (2024八下·慈溪期中) 某学校为了了解本校1200名学生的课外阅读的情况，现从各年级随机抽取了部分学生，对他们一周的课外阅读时间进行了调整，井绘制出如下的统计图①和图②，根据相关信息，解答下列问题：
1. （1）本次接受随机抽样调查的学生人数为，图①中 $\text{[math]}$ 的值为；
2. （2）求本次调查获取的样本数据的众数、中位数和平均数；
3. （3）根据样本数据，估计该校一周的课外阅读时间大于 $\text{[math]}$ 的学生人数．
答案解析收藏纠错 + 选题
19. 某校为了普及环保知识，从七、八两个年级中各选出10名学生参加环保竞赛（满分 100 分)，并对成绩进行整理分析，得到如下信息：

平均数
众数
中位数
七年级参赛学生成绩
85.5
m
87
八年级参赛学生成绩
85.5
85
n
根据以上信息，回答下列问题：
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$
2. （2）七、八年级参䅗学生成绩的方差分别记为 $\text{[math]}$ ， $\text{[math]}$ ，请判断 $\text{[math]}$ $\text{[math]}$ ． (填“ $\text{[math]}$ " $\text{[math]}$ 或 $\text{[math]}$
3. （3）从平均数和中倠数的角度分析，哪个年级参赛学生的成绩较好．
答案解析收藏纠错 + 选题
20. (2024·巧家模拟) 为了解某市生产相同零件的甲、乙两个工厂的工人生产能力情况，决定对其进行抽样调查．现从甲、乙两个工厂各随机抽取了10名工人某天每人加工零件的个数，并对数据进行整理、描述和分析，下面给出了部分信息．
信息一：甲工厂10名工人当天每人加工零件的个数为48，52，44，42，48，46，52，48，43，a ．
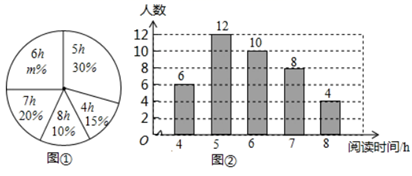
信息二：乙工厂10名工人当天每人加工零件个数频数分布直方图如下图所示．
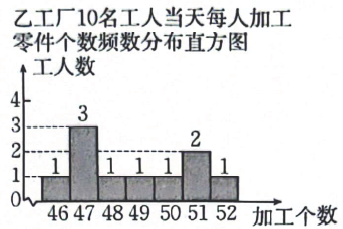
抽取的甲、乙两个工厂工人当天每人加工零件个数的平均数、众数、中位数情况如下表所示：
工厂
平均数
众数
中位数
甲
47.7
b
48
乙
48.8
47
c
根据以上信息，解答下列问题：
1. （1） $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
2. （2）若甲、乙两工厂的总人数相同，则估计当天（填“甲工厂”或“乙工厂”）工人加工的零件个数更多，理由（只填一个）：．
3. （3）若当天加工零件个数达到或超过50个，视为生产能手．若甲、乙两工厂各有1000名工人，试估计当天甲、乙两工厂生产能手的总人数之和．
答案解析收藏纠错 + 选题

四、综合题

21. (2023八下·凉山期末) 为振兴乡村经济，在农产品网络销售中实行目标管理，根据目标完成的情况对销售员给予适当的奖励，某村委会统计了15名销售员在某月的销售额（单位：万元），数据如下：10，4，7，5，4，10，5，4，4，18，8，3，5，10，8
1. （1）补全月销售额数据的条形统计图．
2. （2）月销售额在哪个值的人数最多（众数）？中间的月销售额（中位数）是多少？平均月销售额（平均数）是多少？
3. （3）根据（2）中的结果，确定一个较高的销售目标给予奖励，你认为月销售额定为多少合适？
答案解析收藏纠错 + 选题
22. (2024·威远模拟) 教育部在《大中小学劳动教育指导纲要（试行）》中明确要求：初中生每周课外生活和家庭生活中，劳动时间不少于3小时．某走读制初级中学为了解学生劳动时间的情况，对学生进行了随机抽样调查，并将调查结果制成不完整的统计图表，如图：
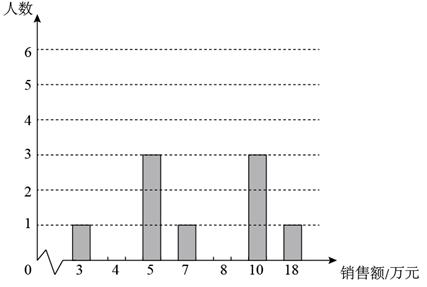
平均每周劳动时间的频数统计表
劳动时间小时
频数
t＜3
9
3≤t＜4
a
4≤t＜5
66
t≥5
15
请根据图表信息，回答下列问题．
1. （1）参加此次调查的总人数是人，频数统计表中a＝；
2. （2）在扇形统计图中，D组所在扇形的圆心角度数是°；
3. （3）该校准备开展以“劳动美”为主题的教育活动，要从报名的2男2女中随机挑选2人在活动中分享劳动心得，请用树状图或列表法求恰好抽到一名男生和一名女生的概率．
答案解析收藏纠错 + 选题
23. (2023·广东模拟) 为了倡导保护资源节约用水，从某小区随机抽取了50户家庭，调查了他们5月的用水量情况，发现每户用水量在 $\text{[math]}$ 吨之间，结果如图所示.
1. （1）这50户家庭中5月用水量在 $\text{[math]}$ 的有多少户？
2. （2）把图中每组用水量的值用该组的中间值（如 $\text{[math]}$ 的中间值为5）来代替，估计该小区平均每户用水量；
3. （3）从该50户用水量在 $\text{[math]}$ 的家庭中，任抽取2户，用树状图或表格法求至少有1户用水量在 $\text{[math]}$ 的概率.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

（通用版）2024年中考数学重点知识冲刺训练---统计与概率

副标题：

*注意事项：

（通用版）2024年中考数学重点知识冲刺训练---统计与概率

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

	平均数	众数	中位数
七年级参赛学生成绩	85.5	m	87
八年级参赛学生成绩	85.5	85	n

数字	0	1	2	3	4	5	6	7	8	9
频数	8	8	12	11	10	8	9	8	12	14

“偏瘦”	“标准”	“超重”	“肥胖”
80	350	46	24

工厂	平均数	众数	中位数
甲	47.7	b	48
乙	48.8	47	c

劳动时间小时	频数
t＜3	9
3≤t＜4	a
4≤t＜5	66
t≥5	15